《高等数学》课程教学资源（PPT课件，上册）微分中值定理

山东农业大 主计 苏本堂 第三章微分中值定理与导数的应用 第一节 微分中值定理 第二节 洛必达法则 第三节 泰勒公式 第四节 函数的单调性与曲线的凹凸性 第五节 函数的极值与最大值最小值 第六节 函数图形的描绘 第七节 曲率

山东农业大学 高等数学 主讲人：苏本堂 第三章 微分中值定理与导数的应用 第一节 微分中值定理 第二节 洛必达法则 第三节 泰勒公式 第四节 函数的单调性与曲线的凹凸性 第五节 函数的极值与最大值最小值 第七节 曲率 第六节 函数图形的描绘

第一节 微分中值定理 罗尔定理 拉格朗日定理 柯西定理

山东农业大学 高等数学 主讲人：苏本堂 第一节 微分中值定理 罗尔定理 拉格朗日定理 柯西定理

苏本堂 一、罗尔(Rolle)定理 费马(ferma)引理 y=f)在U(o)有定义，三f(o)=0 且f(x)≤f(xo),∫'(xo)存在 (或≥) 证：设V0+△r∈U(xo),f(x0+△r)≤f(xo), (xo)=lim fo+Av)-f(xo) △x→0 △x 「'(xo)≥0（△x→0） >f'(xo)=0 f(xo)≤0（△x→0*） 毕

山东农业大学 高等数学 主讲人：苏本堂 费马(fermat)引理 一、罗尔( Rolle )定理 且 存在 (或) 证: 设 则  0  0 x y o 0 x 证毕

罗尔（Rolle)定理 y=f(x)满足： y=f(x) (1)在区间[a,b]上连续 B (2)在区间(a,b)内可导 (3)f(a)=f(b) >在(a,b)内至少存在一点5，使f'(5)=0 证：因f(x)在[a,b]上连续，故在[a,b]上取得最大值 M和最小值m. 若M=m,则f(x)=M,x∈[a,b], 因此5∈(a,b),f'(5)=0

山东农业大学 高等数学 主讲人：苏本堂 罗尔（ Rolle ）定理 满足: (1) 在区间 [a , b] 上连续 (2) 在区间 (a , b) 内可导 (3) f ( a ) = f ( b ) 使 f () = 0. 证: 故在[ a , b ]上取得最大值 M 和最小值 m . 若 M = m , 则 因此 在( a , b ) 内至少存在一点

11。 若M>m,则M和m中至少有一个与端点值不等， 不妨设M≠f(a),则至少存在一点5∈(a,b),使 f(5)=M,则由费马引理得f'(5)=0. 注意： 1)定理条件条件不全具备，结论不一定成立.例如， x=1 f(x)= f(x)=x x∈[-1,1] x∈[0,1] 2)通常称导数为零的点为函数的驻点（或稳定点)

山东农业大学 高等数学 主讲人：苏本堂 若 M > m , 则 M 和 m 中至少有一个与端点值不等, 不妨设 则至少存在一点 使 f () = 0. 注意: 1) 定理条件条件不全具备, 结论不一定成立. 例如, 1 x y o 则由费马引理得 1 x y −1 o 1 x y o 2) 通常称导数为零的点为函数的驻点（或稳定点）

例1.证明方程x5-5x+1=0有且仅有一个小于1的 正实根 证：1)存在性. 设f(x)=x5-5x+1,则f(x)在[0,1]连续，且 f(0)=1,f(①)=-3.由介值定理知存在x∈(0,1)，使 f(xo)=0,即方程有小于1的正根x0 2)唯一性. 假设另有x∈(0,1)，≠xo,使f(x)=0,:f(x)在以 0,1为端点的区间满足罗尔定理条件，.在0，x1之间 至少存在一点5，使f'(5)=0. 但f'(x)=5(x4-1)<0,x∈(0,1)，矛盾，故假设不真！

山东农业大学 高等数学 主讲人：苏本堂 例1. 证明方程 ( ) 5 1, 5 f x = x − x + ( ) 0, f x0 = 有且仅有一个小于1 的 正实根 . 证: 1) 存在性 . 则 f (x) 在 [0 , 1 ] 连续 , 且 由介值定理知存在 (0,1), x0  使 即方程有小于1 的正根 2) 唯一性 . 假设另有  f (x)在以 0 1 x , x 为端点的区间满足罗尔定理条件 , 在x0 , x1之间 至少存在一点 但 矛盾, 故假设不真! 设

例2.设f(x)∈C[0,π]，且在(0，π)内可导，证明至少存 在-点5e(0,π)，使f'(5)sin5=-f(5)cos5. 分析：要证∫"(5)sin5+f(5)cos5=0 [f(x)sinx]-=0 即 证明设F(x)=f(x)sinx 容易验证证F(x)在[0，π]上满足罗尔定理条件 由罗尔定理定理得至少存在一个飞，使得 F(ξ)=0 即 f'(5)sin5+f(5)cos5=0. 从而f'(5)sin5=-f(5)cos5

山东农业大学 高等数学 主讲人：苏本堂 例2. 设 f (x)C[0, ], 且在 (0, ) 内可导, 证明至少存 在一点  (0, ), 使 f ( )sin  = − f ( )cos . 分析: 要证 即  ( )sin  = 0  x= f x x 容易验证证 F(x) 在 [0, ] 上满足罗尔定理条件. 证明 设 F(x) = f (x)sin x 由罗尔定理定理得.至少存在一个, 使得 F( ) = 0 即 f ( )sin  + f ( )cos = 0. 从而 f ( )sin  = − f ( )cos

二、拉格朗日中值定理 观察与思考 设连续光滑的曲线y=孔x)在端点A、B处的纵坐标不 相等. 问题： 直线AB的斜率=？f'(x)=? 提示： yfx) 直线AB的斜率 k=Ib)-f(a) b-a (g)-b)-I(a) a 6 b-a

山东农业大学 高等数学 主讲人：苏本堂 二、拉格朗日中值定理 •观察与思考 设连续光滑的曲线y=f(x)在端点A、B处的纵坐标不 相等 问题： 直线AB的斜率k=? f (x)=? 提示： f ()= b a f b f a − ( )− ( )  k= b a f b f a − ( )− ( ) , 直线AB的斜率

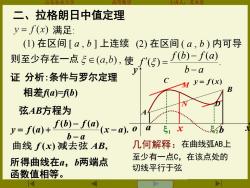
山东农业大 二、拉格朗日中值定理 y=∫(x)满足： (1)在区间[a,b]上连续(2)在区间(a,b)内可导 则至少存在一点5∈(a,),使f)=fb)-f@ b-a 证分析：条件与罗尔定理 My=f(x) 相差f孔a)=fb) 弦AB方程为 y-f(a)+f(b)-f(a(x-a.od .b b-a 曲线f(x)减去弦AB, 几何解释：在曲线弧AB上 所得曲线在a,b两端点 至少有一点C,在该点处的 切线平行于弦 函数值相等

山东农业大学 高等数学 主讲人：苏本堂 二、拉格朗日中值定理 (1) 在区间 [ a , b ] 上连续 满足: (2) 在区间 ( a , b ) 内可导 则至少存在一点 使 . ( ) ( ) ( ) b a f b f a f − −   = a o 1 x  2 b x y y = f (x) A B C N D M 证 分析:条件与罗尔定理 弦AB方程为 ( ). ( ) ( ) ( ) x a b a f b f a y f a − − − = + 曲线 f (x) 减去弦 AB, 相差f(a)=f(b) 所得曲线在a，b两端点 函数值相等。 几何解释：在曲线弧AB上 至少有一点C，在该点处的 切线平行于弦

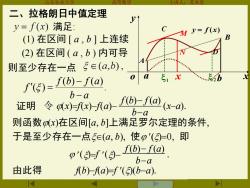
二、拉格朗日中值定理 y=f(x)满足： y=f(x) (1)在区间[a,b]上连续 (2)在区间(a,b)内可导 则至少存在一点5∈(a,b), f"5的)=fb)-fa) b-a 证明令x)Ra)-(b))f@(-a. b-a 则函数x)在区间[a,b]上满足罗尔定理的条件， 于是至少存在一点∈(a,b),使p'()=0,即 9g)-Ka b-a 由此得 b)-a=f'((b-a) M

山东农业大学 高等数学 主讲人：苏本堂 二、拉格朗日中值定理 (1) 在区间 [ a , b ] 上连续 满足: (2) 在区间 ( a , b ) 内可导 则至少存在一点 . ( ) ( ) ( ) b a f b f a f − −   = a o 1 x  2 b x y y = f (x) A B C N D M 则函数j(x)在区间[a, b]上满足罗尔定理的条件, 于是至少存在一点(a, b), 使j ()=0, 即 证明 由此得 f(b)−f(a)=f ()(b−a) 令 j(x)=f(x)−f(a)− b a f b f a − ( )− ( ) (x−a) j ()=f ()− b a f b f a − ( )− ( ) 