《高等数学》课程教学资源（PPT课件，上册）不定积分的概念与性质

山东农大学 高等数学 讲人：本蜀 第四章不定积分 第一节 不定积分的概念与性质 第二节 换元积分法 第三节 分部积分法公式 第四节 有理函数的积分 第五节 积分表的使用

山东农业大学 高等数学 主讲人：苏本堂 第四章 不定积分 第一节 不定积分的概念与性质 第二节 换元积分法 第三节 分部积分法公式 第四节 有理函数的积分 第五节 积分表的使用

第一节不定积分的概念与性质 原函数与不定积分的概念 基本积分表 不定积分的性质

山东农业大学 高等数学 主讲人：苏本堂 第一节 不定积分的概念与性质 原函数与不定积分的概念 基本积分表 不定积分的性质

一、原函数与不定积分的概念 引例：一个质量为m的质点，在变力F=Asint的作 下沿直线运动，试求质点的运动速度v(t) 根据牛顿第二定律，加速度al)=F-4sin( mm 因此问题转化为：已知0=Asint,求0=？ m 定义1.若在区间I上定义的两个函数F(x)及f(x) 满足F'(x)=f(x)或dF(x)=f(x)d,则称F(x)为f(x) 在区间I上的一个原函数. 如引例中，4sint的原函数有-4cos1,-4cost+3, A。 m m m

山东农业大学 高等数学 主讲人：苏本堂 一、 原函数与不定积分的概念 引例: 一个质量为 m 的质点, 下沿直线运动, 因此问题转化为:已知 ( ) sin t , m A v  t = 求 v(t) = ? 在变力 试求质点的运动速度 根据牛顿第二定律, 加速度 定义 1 . 若在区间 I 上定义的两个函数 F (x) 及 f (x) 满足 在区间 I 上的一个原函数 . 则称 F (x) 为f (x) 如引例中, t m A sin 的原函数有 cos t, m A − − cost + 3, m A

问题： 1.在什么条件下，一个函数的原函数存在？ 2.一个函数的原函数是否唯一，若不唯一它们之间 有什么联系？ 3.若原函数存在，它如何表示？ 关于(1)即原函数存在性，我们有 定理1.若函数x)在区间I上连续，则x)在I上存在 原函数. (下章证明) 由于初等函数在其定义域上是连续的，所以得： 初等函数在定义区间上有原函数

山东农业大学 高等数学 主讲人：苏本堂 问题: 1. 在什么条件下, 一个函数的原函数存在 ? 3. 若原函数存在, 它如何表示 ? 定理1.若函数f(x)在区间I上连续,则f(x)在I上存在 原函数 . 由于初等函数在其定义域上是连续的, 所以得: 初等函数在定义区间上有原函数 2. 一个函数的原函数是否唯一, 若不唯一它们之间 有什么联系？ 关于(1) 即原函数存在 性,我们有 (下章证明)

定理2若Fx)是孔x)的一个原函数，则x)所有的原 函数可表示为Fx+C.(C为任意常数) 证：1)(F(x)+C)'=F'(x)=f(x) ∴.F(x)+C是f(x)的原函数 2)设Φ(x)是f(x)的任一原函数，即 Φ'(x)=f(x) 又知 F'(x)=f(x) ∴.[Φ(x)-F(x)]'=Φ'(x)-F'(x)=f(x)-f(x)=0 故 Φ(x)=F(x)+C(C0为某个常数) 即Φ(x)=F(x)+Co

山东农业大学 高等数学 主讲人：苏本堂 证: 1) 又知  [(x) − F(x)] = (x) − F(x) = f (x) − f (x) = 0 故 0 (x) = F(x) +C ( ) C0为某个常数 即 0 (x) = F(x) +C 即 定理2 若F(x)是f(x)的一个原函数, 则f(x)所有的原 函数可表示为F(x)+C . ( C 为任意常数 )

定义2.f(x)在区间I上的原函数全体称为f(x)在I 上的不定积分，记作f(x)dx,其中 ∫一积分号；f()一被积函数； x一积分变量；f(x)d一被积表达式， 若F'(x)=f(x),则 「f(x)dr=F(x)+C(C为任意常数) 例如， 「e'dx=ex+C C称为积分常数 ∫x2dr=}x3+C 不可丢！ sin xdx=-cos x+C

山东农业大学 高等数学 主讲人：苏本堂 定义 2. 在区间 I 上的原函数全体称为 上的不定积分, 其中 — 积分号; — 被积函数; — 积分变量; — 被积表达式. 若 则 ( C 为任意常数 ) C 称为积分常数 不可丢 ! 例如, =  e x x d e C x + =  x dx 2 x +C 3 3 1 =  sin xdx − cos x +C 记作

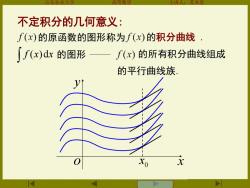
不定积分的几何意义： ∫(x)的原函数的图形称为f(x)的积分曲线· ∫f(x)dx的图形 f(x)的所有积分曲线组成 的平行曲线族 Xo

山东农业大学 高等数学 主讲人：苏本堂 不定积分的几何意义: 的原函数的图形称为 f (x)dx  的图形 的所有积分曲线组成 的平行曲线族. y o x0 x 的积分曲线

山东农业大 方本堂 如果Fx)是fx)的一个原函数，则「fx)dc=F(x)+C. 例1求函数fx)=的不定积分 解当0时，仙y ∫.dk=lnx+C(x0: 当0时，n(-r=(-)= ∫ck=ln(-)+C(r<0. 合并上面两式，得到 ∫1dk=lnlx+C(o40)

山东农业大学 高等数学 主讲人：苏本堂 解：当 x>0 时 (ln x) x 1 =  例 2. 求函数 x f x 1 例1 ( )= 的不定积分 合并上面两式, 得到 解 如果F(x)是f(x)的一个原函数, 则  f (x)dx = F(x)+C  dx x C x = +  ln 1 (x>0) 当 x<0 时 [ln(−x)] x x 1 ( 1) 1  − = − =  dx x C x = − +  ln( ) 1 (x<0) dx x C x = +  ln| | 1 (x0)

例2设曲线通过点(1,2)，且其上任一点处的切线斜率 等于这点横坐标的两倍，求此曲线的方程 解设所求的曲线方程为y=孔x),则曲线上任一点(x,y) 处的切线斜率为 y'=f'(x)=2x, (1,2) 即x)是2x的一个原函数.因为 ∫2xd=x2+C, 故必有某个常数C使孔x)=x2+C,即曲线方程为y=x2+C 因所求曲线通过点(1,2)，故 2=1+C,C=1. 于是所求曲线方程为y=x2+1

山东农业大学 高等数学 主讲人：苏本堂 例2 设曲线通过点(1, 2), 且其上任一点处的切线斜率 等于这点横坐标的两倍, 求此曲线的方程. 故必有某个常数C使f(x)=x 2+C, 即曲线方程为y=x 2+C. 因所求曲线通过点(1, 2), 故 2=1+C, C=1. 于是所求曲线方程为y=x 2+1. 因为  xdx = x +C 2 2  y o x (1, 2) 解 设所求的曲线方程为y=f(x), 则曲线上任一点(x, y) 处的切线斜率为 y=f (x)=2x, 即f(x)是2x 的一个原函数

山东农业大 微分与积分的关系 从不定积分的定义可知 a=,或-f: 又由于Fx)是F'(x)的原函数，所以 ∫F(x)dr=F(x)+C,或记作「dF(x)=F(x)+C. 由此可见，如果不计任意常数，则微分运算与求不定 积分的运算是互逆的 由于积分运算是微分运算的逆运算，由导数公式可 以得到相应的积分公式

山东农业大学 高等数学 主讲人：苏本堂 微分与积分的关系 从不定积分的定义可知 又由于F(x)是F (x)的原函数, 所以 由此可见, 如果不计任意常数, 则微分运算与求不定 积分的运算是互逆的.  [ f (x)dx]= f (x) dx d  或  d[ f (x)dx]= f (x)dx   [ f (x)dx]= f (x) dx d  或  d[ f (x)dx]= f (x)dx   F(x)dx = F(x)+C  或记作 dF(x)= F(x)+C   F(x)dx = F(x)+C  或记作 dF(x)= F(x)+C  由于积分运算是微分运算的逆运算, 由导数公式可 以得到相应的积分公式