《高等数学》课程教学资源（PPT课件，上册）可分离变量的微分方程

山东农业大学 高等数学 主讲人：本堂 第二节可分离变量的微分方程 可分离变量方程 =f)y) dx M(x)M2(y)dx+N(x)N2(y)dy=0 解分离变量方程g(y)dy=f(x)dx

山东农业大学 高等数学 主讲人：苏本堂 第二节可分离变量的微分方程 解分离变量方程 g(y)dy = f (x)dx 可分离变量方程 ( ) ( ) d d 1 2 f x f y x y = M1 (x) M (y) dx + N 1 (x) N (y)d y = 0 2 2

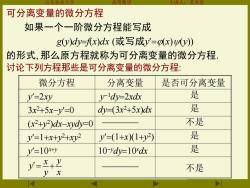
可分离变量的微分方程 如果一个一阶微分方程能写成 gy)dy=x)dk(或写成y=(x)vy) 的形式，那么原方程就称为可分离变量的微分方程 讨论下列方程那些是可分离变量的微分方程： 微分方程 分离变量 是否可分离变量 y'=2xy y-dy=2xdx 是 3x2+5x-y'=0 dy=(3x2+5x)dx 是 (x2+y2)dx-xydy=0 不是 y'=1+x+y2+xy2 y'=(1+x)(1+y2) 是 y'=10+y 10-'dy=10'dx 是 y'=x+业 y x 不是

山东农业大学 高等数学 主讲人：苏本堂 微分方程 分离变量 是否可分离变量 y=2xy 3x 2+5x−y=0 (x 2+y 2 )dx−xydy=0 y=1+x+y 2+xy2 y=10x+y 如果一个一阶微分方程能写成 g(y)dy=f(x)dx (或写成y=(x)(y)) 的形式 那么原方程就称为可分离变量的微分方程 可分离变量的微分方程 讨论下列方程那些是可分离变量的微分方程: x y y x y  = + 是 不是 不是 是 是 是 y −1dy=2xdx dy=(3x 2+5x)dx y=(1+x)(1+y 2 ) 10−ydy=10xdx ———— ————

可分离变量的微分方程 如果一个一阶微分方程能写成 g0y)dy=x)dx(或写成y=o(x)y) 的形式，那么原方程就称为可分离变量的微分方程. 可分离变量的微分方程的解法 分离变量：将方程写成gy)dy=孔x)dx的形式； 两端积分：∫gO=∫fx),设积分后得G0以F心r+C 求显式解：求方程由Gy)=F(x)十C所确定的隐函数 y=Fx)或x=Yy) 方程Gy)=Fx)+C,F(x)或x=Yy)都是方程的通解， 其中Gy)=F(x)+C称为隐式（通）解

山东农业大学 高等数学 主讲人：苏本堂 可分离变量的微分方程的解法 两端积分: 方程G(y)=F(x)+C y=F(x)或x=Y(y)都是方程的通解 其中G(y)=F(x)+C称为隐式(通)解 求显式解: 求方程由G(y)=F(x)+C所确定的隐函数 y=F(x)或x=Y(y) 如果一个一阶微分方程能写成 g(y)dy=f(x)dx (或写成y=(x)(y)) 的形式 那么原方程就称为可分离变量的微分方程 可分离变量的微分方程 分离变量: 将方程写成g(y)dy =f(x)dx的形式   g(y)dy= f (x)dx  设积分后得 G(y)=F(x)+C   g(y)dy= f (x)dx  设积分后得 G(y)=F(x)+C

方本 例1.求微分方程 =3x2y的通解 dx 解：分离变量得 dy y=3x2 dx 说明：在求解过程中 每一步不一定是同解 两边积分j山 变形，因此可能增、 减解 得 Iny=x3+C 或 即 y=te*+C=teCie* 令C=±e9 Iny =x3+In C D=Cex3 (C为任意常数) (此式含分离变量时丢失的解y=0)

山东农业大学 高等数学 主讲人：苏本堂 例1. 求微分方程 的通解. 解: 分离变量得 x x y y 3 d d 2 = 两边积分 得 1 3 ln y = x +C ln y x ln C 3 = + 即 C1 令C = e ( C 为任意常数 ) 或 说明: 在求解过程中 每一步不一定是同解 变形, 因此可能增、 减解. ( 此式含分离变量时丢失的解 y = 0 )

xydx+(x2+1)dy=0 例2.解初值问题 0)=1 解：分离变量得 dy= y d 两边积分得lny=ln +In C 即 y/x2+1=C (C为任意常数) 由初始条件得C=1,故所求特解为 yWx2+1=1

山东农业大学 高等数学 主讲人：苏本堂 例2. 解初值问题 d ( 1) d 0 2 xy x + x + y = 解: 分离变量得 x x x y y d 1 d 2 + = − 两边积分得 即 y x +1 = C 2 由初始条件得C = 1, 1 1 2 y x + = ( C 为任意常数 ) 故所求特解为 y(0) =1

主讲人：苏本学 例3.求下述微分方程的通解： y'=sin2(-y+1) 解：令u=x-y+1,则 u'=1-y' 故有 1-u'=sin2 u 即 sec2 udu dx 解得 tan u x+C 所求通解：tan(x-y+1)=x+C(C为任意常数)

山东农业大学 高等数学 主讲人：苏本堂 例3. 求下述微分方程的通解: 解: 令 u = x − y +1, 则 故有 u u 2 1−  = sin 即 解得 tanu = x +C 所求通解 tan(x − y +1) = x +C ( C 为任意常数 ) :

练习：求方程 dy=exty 的通解， dx 解法1分离变量eydy=edx -er=ex+C 即 (ex+C)e'+1=0(C<0) 解法2令u=x+y,则u'=1+y 故有 u'=1+e“ 积分 du 1+e u-ln(1+e“)=x+C 所求通解：ln(1+e+)=y-C(C为任意常数)

山东农业大学 高等数学 主讲人：苏本堂 练习: 解法 1 分离变量 e e C y x − = + − 即 ( + ) +1 = 0 x y e C e ( C < 0 ) 解法 2 令u = x + y, 故有 u u  =1+ e 积分 u e x C u − ln (1+ ) = + 所求通解: e y C ( C 为任意常数 ) x y + = − + ln (1 ) u e e e u u u d 1 (1 )  + + −

山东农业大 主计 本堂 例4.已知放射性元素铀的衰变速度与当时未衰变原 子的含量M成正比，已知t=0时铀的含量为Mo,求在 衰变过程中铀含量M()随时间t的变化规律 dM =-元M(>0) 解：根据题意，有 dt M=o=M0(初始条件) 对方程分窝变量然后积分-小-2： 得lnM=-t+lnC,即M=Cet +M 利用初始条件，得C=M0 Mo 故所求铀的变化规律为M=Moe21

山东农业大学 高等数学 主讲人：苏本堂 例4. 子的含量 M 成正比, 求在 衰变过程中铀含量 M(t) 随时间 t 的变化规律. 解: 根据题意, 有 ( 0) d d = − M   t M M t=0 = M0 (初始条件) 对方程分离变量, 得 ln M = − t + lnC, 即 t M Ce − = 利用初始条件, 得 C = M0 故所求铀的变化规律为 . 0 t M M e − = M M0 t o 然后积分:   已知 t = 0 时铀的含量为 已知放射性元素铀的衰变速度与当时未衰变原

例5.设降落伞从跳伞塔下落后所受空气阻力与速度 成正比，并设降落伞离开跳伞塔时(t=0)速度为0，求 降落伞下落速度与时间的函数关系 dv 解：根据牛顿第二定律列方程m dt =mg-kv 初始条件为v=0=0 对方程分离变量，然后积分：∫mg一k dv R=kV 得 -是n(mg-k)-+C(此处mg 利用初始条件，得C=-ln(mg) P=mg k 代入上式后化简，得特解v= mg(1-e m

山东农业大学 高等数学 主讲人：苏本堂 例5. 成正比, 求 解: 根据牛顿第二定律列方程 = t v m d d 初始条件为 v t=0 = 0 对方程分离变量, 然后积分   : 得 (此处 mg − kv  0) 利用初始条件, 得 ln ( ) 1 mg k C = − 代入上式后化简, 得特解 并设降落伞离开跳伞塔时( t = 0 ) 速度为0, (1 ) t m k e k m g v − = − mg − kv 设降落伞从跳伞塔下落后所受空气阻力与速度 降落伞下落速度与时间的函数关系. k mg v  t 足够大时

山东农业大 等数 主讲 苏本堂 作业：P.304习题7-2 1(1),(5),(7),(10);2(3),(4)；4;6

山东农业大学 高等数学 主讲人：苏本堂 作业：P- 304习题7-2 1 (1) , (5) , (7) , (10); 2 (3), (4) ; 4 ; 6