《高等数学》课程教学资源（PPT课件，上册）定积分在几何学上的应用

大 人术 第二节定积分在几何学上的应用 平面图形的面积 二 体积 三 平面曲线的弧长

山东农业大学 高等数学 主讲人：苏本堂 第二节 定积分在几何学上的应用 一 平面图形的面积 二 体积 三 平面曲线的弧长

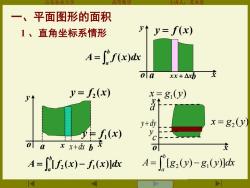
山东农业大 方本 一、平面图形的面积 1、直角坐标系情形 ↑y=f(x) A="f(x)d o a r+△b y=f2(x) x=81y) y+dy x=82y) fi(x) o a 七x+b o A=[Lf(x)-f(x)ld A=[g2(y)-g(y)ldx

山东农业大学 高等数学 主讲人：苏本堂 一、平面图形的面积 x y o y = f (x) a b =  b a A f (x)dx  = − b a A [ f2 (x) f1 (x)]dx xx + x 1 、直角坐标系情形 x y o ( ) y = f 1 x ( ) y = f 2 x a x x + dx b x y o c d ( ) 1 x = g y ( ) 2 x = g y y y + dy  = − b a A [g (y) g (y)]dx 2 1

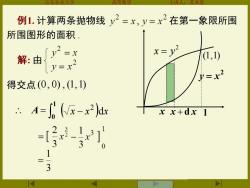
例1.计算两条抛物线y2=x,y=x2在第一象限所围 所围图形的面积 解：由 y-=x (1,1) 2 y=x 得交点(0,0)，(1,1) P=x2 ·A=(x-x2d xx+dx 1 3

山东农业大学 高等数学 主讲人：苏本堂 例1. 计算两条抛物线 在第一象限所围 所围图形的面积 . 2 y = x x x + d x 解: 由 得交点 (0, 0) , (1,1) (1,1) d A ( x x )dx 1 2 = − 3 1 =   = 1 0 A 2 x = y

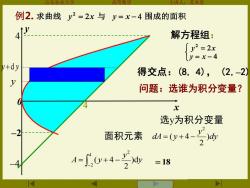
山东农少大 主讲 本堂 例2.求曲线y2=2x与y=x-4围成的面积 解方程组： {y2=2x y=x-4 v+dy 得交点：(8,4)，(2，-2) y 问题：选谁为积分变量？ x 选y为积分变量 面积元素 d1=0y+4-y A=0+4 =18

山东农业大学 高等数学 主讲人：苏本堂 求曲线 =  与 = − 4 围成的面积  y x y x –2 。 。 0 y x 例2. 4 4 –4 解方程组：    = −  =   y x y x 得交点：(8, 4)， (2,–2) 问题：选谁为积分变量？ )d 2 ( 4 2 4 2 y y A = y + − − = 18 选y为积分变量 面积元素 ) 2 ( 4 2 dy y dA = y + − y y + d y

2 例3.求椭圆 2+ =1所围图形的面积. 解：利用对称性，有dA=ydx 4=4dx 利用椭圆的参数方程 x=acost l y=bsint (0≤t≤2π) 应用定积分换元法得 A=4 bsint.(-asint)dt inrd =4ab:2受=xab 当a=b时得圆面积公式

山东农业大学 高等数学 主讲人：苏本堂 a b o x y x 例3. 求椭圆 解: 利用对称性 , d A = y dx 所围图形的面积 . 有  = a A y x 0 4 d 利用椭圆的参数方程 (0 2 ) sin cos       = = t y b t x a t 应用定积分换元法得  = 2 0 2 4 sin d  ab t t = 4ab 2 1  2   =  ab 当 a = b 时得圆面积公式 x + d x

山东农业大 等数 苏本堂 例4.求由摆线x=a(t-sint),y=a(1-cost)(a>0) 的一拱与x轴所围平面图形的面积 解：A=a0-cos)-a1-c0s1dt -a (1-eost)2dr 2 -4d (令u=) 20 =8a2∫sin4udu =16a .31 =3ra2 422

山东农业大学 高等数学 主讲人：苏本堂 例4. 求由摆线 的一拱与 x 轴所围平面图形的面积 . 解: dA = a(1− cost) a(1− cost)d t a (1 cost) d t 2 0 2 2  = −  t t a d 2 4 sin 2 0 2 4  =  ) 2 ( t 8a sin u d u 令u = 0 2 4  =  16a sin u d u 2 0 2 4  =  2 = 3 a  = 2 0 A O 2a y x

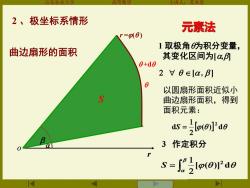
东农 2、极坐标系情形 元素法 r=m(0) 1取极角为积分变量， 曲边扇形的面积 其变化区间为[a例 0+d0 2 V0Ela,B] 以圆扇形面积近似小 曲边扇形面积，得到 面积元素： as-Oo 3作定积分 s=22lo612d0

山东农业大学 高等数学 主讲人：苏本堂 d o   +d r =( ) 元素法 1 取极角为积分变量， 其变化区间为[,] d ( ) d    S = 以圆扇形面积近似小 曲边扇形面积，得到 面积元素：    [ ,  ] .     =   . S [( )] d  曲边扇形的面积 dS S 3 作定积分 . r  2 、极坐标系情形

、本写 例5.计算阿基米德螺线r=a0(a>0)对应0从0变 到2π所围图形面积 2πa p=a0 4 -π1

山东农业大学 高等数学 主讲人：苏本堂 例5. 计算阿基米德螺线 对应  从 0 变 解:  d (  ) d 2 1 2 a  = 2 0 A 2 2 a =       3 3 1  0 2 3 2 3 4 =  a 到 2 所围图形面积

例6.计算心形线=a(1+cos0)(a>0)所围图形的 面积· 解：4=2020+c0w0Yd0 (利用对称性) π ,4 r=a(1+cose) 2 令1=号 2a =8a2.3.1.3 4222

山东农业大学 高等数学 主讲人：苏本堂 8a cos t dt 2 0 2 4  =  例6. 计算心形线 所围图形的 面积 . 解: (1 cos ) d 2 1 2 2 a +  =  0 2 a   d 2 4cos4 (利用对称性) 2  令t = =  2 8a  4 3  2 1 2  2 2 3 =  a d  r = a(1+ cos ) 2a

例7.计算心形线r=a(1+cos0)(a>0)与圆r=a 所围图形的面积 解：利用对称性，所求面积 2+2g2a2+co0 4- 2 1 (+2c+cos20)d0 a2+a273 2 1 3 +☑ 2(π-2) 2 2ax 2a1 4

山东农业大学 高等数学 主讲人：苏本堂   2 1+ 2cos + cos (1 cos 2 ) 2 1 +  o a 2a x y (1 cos ) d 2 1 2 2 +  a 例7. 计算心形线 与圆 所围图形的面积 . 解: 利用对称性 , + 2 2 2 1 A =  a  = + 2 2 2 1  a a  cos 2 )d 2 1 2cos 2 3 ( + + 所求面积 2) 4 3 ( 2 1 2 2 =  a + a  −