《高等数学》课程教学资源（PPT课件，下册）第八章 习题课

第八章总结 一、主要内容 二、实例分析

山东农业大学 高等数学 主讲人：苏本堂 第八章总结 一、主要内容 二、实例分析

等数学 主进 本堂 向量运算 a=(ax;ay,a:),b=(bx:by:b),=(Cx:cy,c=) 1.向量运算 加减： a±b=(a±bx,a±by,a:±b:) 数乘： a=(⑦ax,ay,2a) 点积： a.B=abx+a,by+ab. i了 叉积： axb- ax ay a- bx by b=

山东农业大学 高等数学 主讲人：苏本堂 向量运算 设 1. 向量运算 加减: 数乘: 点积: ( , , ) x x y y z z a  b = a  b a  b a  b ( , , ) x y z  a = a a a x x y y z z a b = a b + a b + a b ( , , ) , ( , , ), ( , , ) x y z x y z x y z a = a a a b = b b b c = c c c 叉积: i j k ax y a az bx y b z b ab =

向量积的行列式计算法 axb=(ayb-a.by)i+(a.bx-axb-)j +(axby-aybx)k a-axi+ay j+ak ax ay a 万=bi+b,j+b bx by 9

山东农业大学 高等数学 主讲人：苏本堂 向量积的行列式计算法 i j k = ax y a az bx y b z b , x z x z b b a a − a b a b i y z z y ( − ) a b a b j z x x z + ( − ) a b a b k x y y x + ( − ) a a i a j a k = x + y + z b b i b j b k = x + y + z

方本堂 ax ay a 混合积：[abc]=(a×b)c= bx by Cx Cy Cz 2.向量关系： al/=0 by b. x a d16=a-b=0=ab+ab,+a,b.=0 a,b,c共面二(a×b)c=0 ax a a b 6 =0 x Cy

山东农业大学 高等数学 主讲人：苏本堂 混合积: 2. 向量关系: = x x a b = y y a b z z a b + + = 0 x x y y z z a b a b a b x y z x y z x y z c c c b b b a a a  a b c = ( ab ) c = a,b,c共面 = 0 x y z x y z x y z c c c b b b a a a ( ab ) c = 0 ab = 0

空间曲面 1.空间曲面一三元方程F(x,y,z)=0 ·球面(x-0)2+(y-0)2+(2-0)2=R2 ●旋转曲面 如，曲线 = x=0 绕z轴的旋转曲面： f±Vx2+y2,z)=0 。柱面 如，曲面F(x,y)=0表示母线平行z轴的柱面 又如，椭圆柱面，双曲柱面，抛物柱面等·

山东农业大学 高等数学 主讲人：苏本堂 空间曲面 1. 空间曲面 三元方程 F(x, y , z) = 0 • 球面 2 2 0 2 0 2 0 (x − x ) + ( y − y ) + (z − z ) = R • 旋转曲面 如, 曲线    = = 0 ( , ) 0 x f y z 绕 z 轴的旋转曲面: ( , ) 0 2 2 f  x + y z = • 柱面 如,曲面 F(x, y) = 0 表示母线平行 z 轴的柱面. 又如,椭圆柱面, 双曲柱面, 抛物柱面等

兰订 主讲 苏本堂 2.二次曲面一三元二次方程 2 ·椭球面 b3 c ·抛物面 椭圆抛物面 双曲抛物面 (p,9同号) x2.y2 ,y2 =Z 2P 2q 2p 2q ·双曲面： 单叶双曲面 双叶双曲面 2 2 62 e2=1 62 ·椭圆锥面：

山东农业大学 高等数学 主讲人：苏本堂 2. 二次曲面 三元二次方程 ( p,q同号) • 椭球面 • 抛物面: 椭圆抛物面 双曲抛物面 z q y p x + = 2 2 2 2 • 双曲面: 单叶双曲面 2 2 2 2 b y a x + =1 双叶双曲面 2 2 2 2 b y a x + = −1 • 椭圆锥面: 2 2 2 2 2 z b y a x + =

空间曲线 空间曲线可视为两曲面的交线，其一般方程为方程组 F(x,y,z)=0 G(x,y,z)=0 例如，方程组 G(x,y,z)=0 F(x,y,z)=0 [x2+y2=1 2x+3z=6 表示圆柱面与平面的交线C

山东农业大学 高等数学 主讲人：苏本堂 空间曲线可视为两曲面的交线, 其一般方程为方程组 S2 L F(x, y,z) = 0 G(x, y,z) = 0 S1 例如,方程组 表示圆柱面与平面的交线 C. x z 1 y o C 2 空间曲线

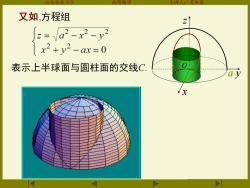
山东农业大 等数学 又如，方程组 ∫z=a2-x2-y2 1x2+y2-ax=0 表示上半球面与圆柱面的交线C 0

山东农业大学 高等数学 主讲人：苏本堂 又如,方程组 表示上半球面与圆柱面的交线C. y x z a

将曲线C上的动点坐标x,y表示成参数t的函数： x=x(f) y=y(t) 称它为空间曲线的 参数方程 2=z(t) 例如，圆柱螺旋线的参数方程为 x=acosot y=asinot 令0=01，b=y x=acos0 z=vt y=asing z=b0 当0=2π时，上升高度h=2πb,称为螺距

山东农业大学 高等数学 主讲人：苏本堂 z x y o 将曲线C上的动点坐标x, y, z表示成参数t 的函数: 称它为空间曲线的 参数方程. 例如,圆柱螺旋线    v 令 = t , b = h = 2 b 的参数方程为 上升高度 , 称为螺距 .  M

本 空间曲线在坐标面上的投影 设空间曲线C的一般方程为 F(x,y,z)=0 G(x,y,z)=0 消去z得投影柱面H(x,y)=0, 则C在xoy面上的投影曲线C为 H(x,y)=0 z=0 消去x得C在y0z面上的投影曲线方程 R(y,2)=0 x=0 消去y得C在zox面上的投影曲线方程 /T(x,2)=0 y=0

山东农业大学 高等数学 主讲人：苏本堂 空间曲线在坐标面上的投影 设空间曲线 C 的一般方程为 消去 z 得投影柱面 则C 在xoy 面上的投影曲线 C´为 消去 x 得C 在yoz 面上的投影曲线方程 消去y 得C 在zox 面上的投影曲线方程    = = 0 ( , ) 0 z H x y    = = 0 ( , ) 0 x R y z    = = 0 ( , ) 0 y T x z z y x C C