《高等数学》课程教学资源（PPT课件，下册）D11.5 对坐标的曲面积分

山东 第五节对坐标的曲面积分 一、对坐标的曲面积分的概念与性质 二、对坐标的曲面积分的计算法 三、两类曲面积分之间的联系

山东农业大学 高等数学 主讲人：苏本堂 第五节 对坐标的曲面积分 一、对坐标的曲面积分的概念与性质 二、对坐标的曲面积分的计算法 三、两类曲面积分之间的联系

山东农业大 对坐标的曲面积分的概念与性质 1.有向曲面及曲面元素的投影 双侧曲面 ·曲面分类 曲面分内侧和 单侧曲面 外侧 莫比乌斯带 曲面分左侧和 曲面分上侧和 (单侧曲面的典型) 右侧 下侧

山东农业大学 高等数学 主讲人：苏本堂 一、对坐标的曲面积分的概念与性质 1.有向曲面及曲面元素的投影 • 曲面分类 双侧曲面 单侧曲面 莫比乌斯带 曲面分上侧和 下侧 曲面分内侧和 外侧 曲面分左侧和 (单侧曲面的典型) 右侧

·指定了侧的曲面叫有向曲面，其方向用法向量指向 表示： 方向余弦 cos a cos B cos y 封闭曲面 侧的规定 >0为前侧 >0为右侧>0为上侧 外侧 0时 类似可规定 当cosy<0时 0 当c0sy=0时 (AS)(AS)

山东农业大学 高等数学 主讲人：苏本堂 其方向用法向量指向 方向余弦 cos cos  cos  > 0 为前侧 0 为右侧 0 为上侧 < 0 为下侧 外侧 内侧 • 设  为有向曲面, ( ) , xy S S (S) xy = 侧的规定 • 指定了侧的曲面叫有向曲面, 表示 : 其面元 在 xoy 面上的投影记为 的面积为 则规定 ( ) ,  xy ( ) , −  xy 0 , 当cos  0时 当cos  0时 当cos  0时 类似可规定 S yz S zx ( ) , ( )

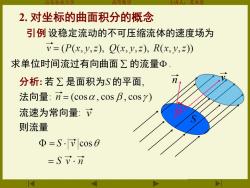
山东农业大 等数 2.对坐标的曲面积分的概念 引例设稳定流动的不可压缩流体的速度场为 v=(P(x,y,2),Q(x,y,2),R(x,y,2) 求单位时间流过有向曲面∑的流量Φ 分析：若∑是面积为S的平面 法向量：n=(cosa,cosB,cosy) 流速为常向量： 则流量 Φ=S.cos0 =Sv.n

山东农业大学 高等数学 主讲人：苏本堂 2. 对坐标的曲面积分的概念 引例 设稳定流动的不可压缩流体的速度场为 求单位时间流过有向曲面  的流量 . S  分析: 若  是面积为S 的平面, 则流量 法向量: 流速为常向量: n v

对一般的有向曲面∑，对稳定流动的不可压缩流体的 速度场V=(P(x,y,z),Q(x,y,2),R(x,y,2) 用“大化小，常代变，近似和，取极限” 2 进行分析可得Φ=lim∑可·n,△S, 2→0 i=l 设i,=(coS,cosB,c0SYi),则 Φ=lim∑[P(5i,i,5i)cos4,+Q(5,n,5i)cosB, 2→01 +R(i,n,i)cosYi ]AS lim 2-→0 [P((S )+()(AS:)s i=1 +R(5,7,5)(△S)xy]

山东农业大学 高等数学 主讲人：苏本堂  对一般的有向曲面 , 用“大化小, 常代变, 近似和, 取极限”  = n i 1 0 lim →  = 0 lim → =   = n i 1  P  i i  i i ( , , )cos R i i i i + ( , , )cos 0 lim → =   = n i 1 Q i i  i  i + ( , , )cos  i S 对稳定流动的不可压缩流体的 速度场 进行分析可得 ni i v i i i v  n S (cos , cos , cos ) i i i i 设 n =     , 则

定义.设∑为光滑的有向曲面，在∑上定义了一个 向量场A=(P(x,y,2),Q(x,y,),R(x,y,)若对Σ的任 意分割和在局部面元上任意取点，下列极限都存在 1im∑[P(5,n,5)AS)yz 2→0 i=l +Q(i,n,i)(ASi)=x+R(si,ni,5i)(ASi)xy] 则称此极限为向量场A在有向曲面上对坐标的曲面积 分，或第二类曲面积分.记作 [Pdydz+Qd=dx+Rdxdy PQ,R叫做被积函数；∑叫做积分曲面

山东农业大学 高等数学 主讲人：苏本堂 设  为光滑的有向曲面, 在  上定义了一个 意分割和在局部面元上任意取点,  = n i 1 i i i i zx + Q( , , )(S ) 分,  Pdy d z + Qd z d x + Rdxdy 记作 P, Q, R 叫做被积函数;  叫做积分曲面. 或第二类曲面积分. 下列极限都存在 向量场 A = (P(x, y,z), Q(x, y,z), R(x, y,z)), 若对 的任 则称此极限为向量场 A 在有向曲面上对坐标的曲面积 定义

八Pdyd=i称为P在有向曲面∑上对y,z的曲面积分 八Qd=dx称为Q在有向曲面∑上对z,x的曲面积分； 小Rdxdy称为R在有向曲面∑上对x,y的曲面积分. 引例中，流过有向曲面∑的流体的流量为 =[fPdyd=+Qd=dx+Rdxdy 若记∑正侧的单位法向量为n=(cosa,cosB,cosy) ds=nds=(dydz,dzdx,dxdy) A=(P(xy,z),Q(x,y,2),R(x,y,2) 则对坐标的曲面积分也常写成如下向量形式 Pdyd:+Qd=dx+Rdxdy =f 4nds-f4d

山东农业大学 高等数学 主讲人：苏本堂 引例中, 流过有向曲面  的流体的流量为  Pd y d z 称为Q 在有向曲面上对 z, x 的曲面积分;  Rd xd y 称为R 在有向曲面上对 x, y 的曲面积分. 称为P 在有向曲面上对 y, z 的曲面积分;   = Pdy d z + Qd z d x + Rdx dy 若记  正侧的单位法向量为 令 n = (cos , cos  , cos ) d S = nd S = (d yd z, d zd x, d xd y) A = (P(x, y,z),Q(x, y,z),R(x, y,z)) 则对坐标的曲面积分也常写成如下向量形式  Pd y d z + Qd z d x + Rd xd y  = A nd S  = Ad S

山东农业大 3.对坐标的曲面积分的性质 对坐标的曲面积分具有与对坐标的曲线积分类似的 一些性质， (1)如果把S分成S,和S2,则 ∬Pddt+Oddk+Rakd =∬Pddk+Qddx+Rkdr+∬Pddk+Oddk+Rak. (2)设$是有向曲面，S表示与$取相反侧的有向曲面， 则 ∬Pddt+Qd-dx-+Rdkr=-J∬Pddk+Odzdx+Rdky

山东农业大学 高等数学 主讲人：苏本堂 3. 对坐标的曲面积分的性质 对坐标的曲面积分具有与对坐标的曲线积分类似的 一些性质 (1)如果把S分成S1和S2  则 (2)设S是有向曲面 S −表示与S取相反侧的有向曲面 则 Pdydz+Qdzdx +Rdxdy   = Pdydz+Qdzdx +Rdxdy+ Pdydz+Qdzdx +Rdxdy   1 2  Pdydz+Qdzdx +Rdxdy = − Pdydz+Qdzdx +Rdxdy     − 

二、对坐标的曲面积分的计算法 定理：设光滑曲面∑：z=(x,y),(x,y)∈Dxy取上侧， R(x,y,z)是∑上的连续函数，则 ∬sR(x,y,z)dxdy=∬DR(x,yz(x,y》dxdy 证：J小3R(x,y,z)dxdy=Iim∑R(5,5(AS)xw 2→0 i=l Σ取上侧，∴(AS)x=(△o)xy 5i=z(51,7) =1im∑R5,n,z(5,n:》(Ao)xy λ→0 i=1 =o R(x,y,=(x.y))dxdy

山东农业大学 高等数学 主讲人：苏本堂 二、对坐标的曲面积分的计算法 定理: 设光滑曲面 取上侧, 是  上的连续函数, 则  R(x, y,z)d x d y ( , , )  = D x y R x y z(x, y) d xd y 证: 0 lim → =   = n i 1 i xy (S ) i xy ∵ 取上侧 = ( ) , ( , ) i i i  = z   0 lim → =   = n i 1 ( , , ) R i i i xy ( ) R x y z x,y x y Dx y ( , , ( ))d d  =  R(x, y,z)d x d y

说明：如果积分曲面∑取下侧，则 R(x,y,=)dxdy=-p.R(xy,=(x))dxdy ·若Σ：x=x(y,),(y,)∈Dz,则有 八sP(x,y,2)dd=±jD.P(0y,2),yz)dyda (前正后负) ·若∑：y=y(2,),(2,)∈D2x,则有 Q(x.=)d=dx=Q((=.x).z)dzdx (右正左负)

山东农业大学 高等数学 主讲人：苏本堂 • 若 则有  P(x, y,z)d ydz P( , y,z) Dyz  =  x( y,z) d y d z • 若 则有  Q(x, y,z)d z d x ( , , z )  =  Dzx Q x y(z, x) d z d x (前正后负) (右正左负) 说明: 如果积分曲面 取下侧, 则  R(x, y,z)d xd y ( , , )  = − Dx y R x y z(x, y) d xd y