《高等数学》课程教学资源（PPT课件，下册）第十一章 习题课

高 第十一章习题课 基本内容 。典型例题

山东农业大学 高等数学 主讲人：苏本堂 第十一章 习题课 基本内容 典型例题

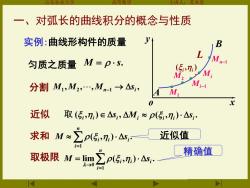
一、对弧长的曲线积分的概念与性质 实例：曲线形构件的质量 B L 匀质之质量M=p·S. M ,:) M2 M 分割M1,M2,.,Mn-1→△S, M-1 A M 0 近似 取(5，n)∈△s,△M;≈p(5,n:)·△s 求和M≈∑p(5,n)Ay, 近似值 精确值 取极限M=im∑p(传，n,)△，. 2→01 i=1

山东农业大学 高等数学 主讲人：苏本堂 一、对弧长的曲线积分的概念与性质 实例:曲线形构件的质量 匀质之质量 M =   s. o x y A B M1 M2 Mi−1 Mi Mn−1 L ( , )  i i 分割 , , , , 1 2 n 1 i M M M → s  − ( , ) , i i i 取    s ( , ) . i i i i M      s 求和 ( , ) . 1 =    n i i i i M    s 近似值 取极限 lim ( , ) . 1 0= → =   n i i i i M    s  精确值 近似

1.定义设L为xOy面内的一条光滑曲线弧，函数fx,y)在L 上有界.将L任意分成n个小弧段：△s1,△s2,··,△sn(△s,也表示 第个小弧段的长度)；在每个小弧段△s上任取一点(5,7)，作和 ∑f5,7)△s; i1 如果当=max{△S1,△s2,··,△sm}→0时，这和的极限总存在，则 称此极限为函数x,y)在曲线弧L上对弧长的曲线积分，记作 ∫fx,即 fxk=m∑f5,n)As, 0≥1 其中x,y)叫做被积函数，L叫做积分弧段

山东农业大学 高等数学 主讲人：苏本堂 1. 定义 设L为xOy面内的一条光滑曲线弧 函数f(x y)在L 上有界将L任意分成n个小弧段s1  s2     sn (si也表示 第i个小弧段的长度)在每个小弧段si上任取一点(i  i ) 作和 i i i n i f s =  ( , ) 1    i i i n i L f x y ds = f s → =  ( , ) lim  ( , ) 1 0     如果当=max{s1  s2     sn }→0时 这和的极限总存在 则 称此极限为函数f(x y)在曲线弧L上对弧长的曲线积分 记作 f x y ds L ( , )   即 其中f(x y)叫做被积函数 L叫做积分弧段

山东 方本 对弧长的曲线积分 f(x.y)ds=m2f5,7)△ 注 元>021 •对弧长的曲线积分也称为第一类曲线积分 ·当函数孔x,y)在光滑曲线弧L上连续时，函数x,y)在曲线 弧L上对弧长的曲线积分是存在的.以后我们总假定孔x,y) 在L上是连续的. 如果L是闭曲线，则记为ff(x,y)ds. ·类似地定义函数孔x,y,z)在空间曲线弧「上对弧长的曲线 积分： f6xy,2)d=lim∑f5,n,5)△s. 2>01

山东农业大学 高等数学 主讲人：苏本堂 i i i n i L f x y ds = f s → =  ( , ) lim  ( , ) 1 0     对弧长的曲线积分 注 •当函数f(x y)在光滑曲线弧L上连续时 函数f(x y)在曲线 弧L上对弧长的曲线积分是存在的 以后我们总假定f(x y) 在L上是连续的 •对弧长的曲线积分也称为第一类曲线积分 i i i i n i f x y z ds = f s → =   ( , , ) lim  ( , , ) 1 0      •类似地定义函数f(x y z)在空间曲线弧上对弧长的曲线 积分 •如果 L 是闭曲线 , 则记为 ( , )d . L f x y s

注 如果L(或Γ)是分段光滑的，则规定函数在L(或T)上的曲 线积分等于函数在光滑的各段上的曲线积分的和， 例如，设L可分成两段光滑曲线弧L及L,则规定 fds-l f.yds+f.ds 思考： (I)若在L上fx,归1，问，ds表示什么？ (2)定积分是否可看作对弧长曲线积分的特例？ 否！对弧长的曲线积分要求ds≥0，但定积分中 dx可能为负

山东农业大学 高等数学 主讲人：苏本堂 •如果L(或)是分段光滑的 则规定函数在L(或)上的曲 线积 分等于函数在光滑的各段上的曲线积分的和 例如 设L可分成两段光滑曲线弧L1及L2  则规定 f x y ds f x y ds f x y ds L L L L ( , ) ( , ) ( , ) 1 2 1 2    = + +  注 思考: (1) 若在 L 上 f (x, y)≡1, 问 d 表示什么? L s (2) 定积分是否可看作对弧长曲线积分的特例 ? 否!对弧长的曲线积分要求 ds  0 , 但定积分中 dx 可能为负

本堂 2.性质 性质1设c1、c2为常数，则 [cf(x.y)+czg(x.y)ds=aJ f(x.yds+c2Jg(x.y)ds; 性质2若积分弧段L可分成两段光滑曲线弧L,和L,则 (ds=J.f(.ds+f(x.ds; 性质3设在L上几x,y)g(x,y),则 fex凼≤gx,b. 特别地，有 f(ds川函

山东农业大学 高等数学 主讲人：苏本堂 2. 性质 性质1 设c1、c2为常数 则 c f x y c g x y ds c f x y ds c g x y ds L L L [ ( , ) ( , )] ( , ) ( , )  1 2 1 2 + = +  性质2 若积分弧段L可分成两段光滑曲线弧L1和L2  则 f x y ds f x y ds f x y ds L L L ( , ) ( , ) ( , ) 1 2    = +  性质3 设在L上f(x y)g(x y) 则    L L f (x, y)ds g(x, y)ds  特别地 有    L L | f (x, y)ds| | f (x, y)|ds

二、对弧长的曲线积分的计算法 基本思路：求曲线积分 转化 计算定积分 定理：设∫(x,y)是定义在光滑曲线弧 L:x=p(t),y=y(t)(a≤t≤B) 上的连续函数，则曲线积分∫，f(x,)d存在，且 Jf.y)ds-SPMo().w(lo2O+v2@)dt 证：根据定义 「2/x,d=m2f低，%A 2→0k-1

山东农业大学 高等数学 主讲人：苏本堂   =  +    f x y ds f  t  t  t  t t L ( , ) [ ( ), ( )] ( ) ( ) d 2 2 二、对弧长的曲线积分的计算法 基本思路: 计算定积分 转 化 定理: 上的连续函数, 且 证: 是定义在光滑曲线弧 则曲线积分 求曲线积分 根据定义 k k n k k =  f s = → lim ( , ) 1 0   

主计 方本堂 因此 f(x,y)ds =∫/Io0).wt小e2)+w2a)d 说明： (I)·△Sk>0,'.△tk>0,因此积分限必须满足<B! (2)注意到 ds=(dx)2+(dy)2 =vo2()+w2(t)dt ds dy dx 因此上述计算公式相当于“换元法”. X

山东农业大学 高等数学 主讲人：苏本堂 dx dy ds x y o 说明: (1)   0,  0, k k  s t 因此积分限必须满足    ! (2) 注意到 2 2 ds = (d x) + (d y) (t) (t) d t 2 2 =  + 因此上述计算公式相当于“换元法”. x 因此

设曲线L的参数方程为x=(),y=()(β)，则 ∫fxys=f几ou,wtp2)+w20d(aK 讨论： (I)若曲线L的方程为=xa≤x≤b),则∫fx,)=？ 2)若曲线L的方程为x=0c≤d,则∫fx,s=? 提示： (1)L的参数方程为x=x,y=x)(a≤x≤b), ∫fx西=x,+26k. (2)L的参数方程为x=00y),=(C≤d), 2 fx.y)ds=-2o0w以o20+id

山东农业大学 高等数学 主讲人：苏本堂 f x y ds f t t t t dt L ( , ) [ ( ), ( )] ( ) ( ) 2  2      =  +    () 设曲线 L的参数方程为x=(t) y=(t) (t) 则 讨论 (1)若曲线 L 的方程为 y=(x)(axb) 则 f x y ds L ( , )  =？ (2)若曲线 L 的方程为 x=(y)(cyd) 则 f x y ds L ( , )  =？ 提示 (1)L的参数方程为x=x y=(x)(axb) f x y ds f x x x dx b L a   ( , ) = [ , ( )] 1+  ( )   2  (2)L的参数方程为x=(y) y=y(cyd) f x y ds f y y y dy d L c   ( , ) = [ ( ), ]  ( )+1 2   

山东农 定理：设f(x,y)是定义在光滑曲线弧 L:x=p(t),y=y(t)(C≤t≤B) 上的连续函数，则曲线积分∫，f(x,)ds存在，且 J.ds-2(+d 推广：设空间曲线弧的参数方程为 T:x=(t),y=w(t),z=o(t)(0≤t≤B) 则Jnf(x,y2)ds -ffv.o)j202+odr

山东农业大学 高等数学 主讲人：苏本堂   =  +    f x y ds f  t  t  t  t t L ( , ) [ ( ), ( )] ( ) ( ) d 2 2 定理: 上的连续函数, 且 是定义在光滑曲线弧 则曲线积分 推广: 设空间曲线弧的参数方程为 : x =(t), y =(t), z =(t) (  t   ) 则  f (x, y,z)ds (t) (t) (t) d t 2 2 2 =   + +   f ((t) ,(t),(t) )