《高等数学》课程教学资源（PPT课件，下册）第十二章习题课

主 办本堂 第十二章习题课 。基本内容 。典型例题

山东农业大学 高等数学 主讲人：苏本堂 第十二章 习题课 基本内容 典型例题

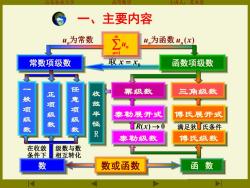
一、主要内容 un为常数 ∑， un为函数un(x) 常数项级数 取X=飞 函数项级数 正 幂级数 三角级数 项 项级数 任意项级 收鲸半 泰勒展开式 傅氏展开式 数 数 R RX>0 满足狄氏条件 泰勒级数 傅氏级数 在收敛 级数与数 条件下 相互转化 数 数或函数 函数

山东农业大学 高等数学 主讲人：苏本堂 常数项级数 函数项级数 一 般 项 级 数 正 项 级 数 收 幂级数 三角级数 敛 半 径 R 泰勒展开式 数 数或函数 函 数 任 意 项 级 数 傅氏展开式 泰勒级数 傅氏级数 R(x) → 0 un为常数 u u (x) n为函数 n 满足狄 氏条件 取 x = x0 在收敛 级数与数 条件下 相互转化   n=1 un 一、主要内容

山东农业大 等数 一、数项级数的审敛法 1.利用部分和数列的极限判别级数的敛散性 2.正项级数审敛法 必要条件lim4n=0 n->∞ 不满足→发散 满足 比值审敛法lim Un+l =p 部分和极限 I n->oo p=不定 比较审敛法 根值审敛法lim/u,=P 用它法判别 n->0 积分判别法 p1 收敛 发散

山东农业大学 高等数学 主讲人：苏本堂 一、数项级数的审敛法 1. 利用部分和数列的极限判别级数的敛散性 2. 正项级数审敛法 必要条件 lim = 0 → n n u 不满足 发 散 满足 比值审敛法 lim n→ un+1 un =  根值审敛法 =  → n n n lim u  1 收 敛 发 散  =1 不定 比较审敛法 用它法判别 积分判别法 部分和极限  1

3.任意项级数审敛法 00 概念：∑4n为收敛级数 n=1 若 ∑4收敛，称∑4n绝对收敛 n=1 n=l 若 ∑4n发散，称∑4n 条件收敛 n=1 n=l Leibniz判别法：若4n≥4n+l>0,且limu,=0, 则交错级数∑(-1)”un收敛，且余项n≤n+1 n=l

山东农业大学 高等数学 主讲人：苏本堂 3. 任意项级数审敛法 为收敛级数 Leibniz判别法: 若 且 则交错级数 收敛 , 概念: 且余项 若 收敛 , 称 绝对收敛 若 发散 , 称 条件收敛

例1.若级数∑an与∑bn均收敛，且an≤cn≤bn n=1 n=l (n=1,2,),证明级数∑cn收敛 n=l 证：0≤cn-an≤bn-an(n=1,2,),则由题设 ∑(bn-an)收敛∑(cn-an)收敛 n=1 n=] n=1 n=1 =∑(cn-an)+∑an收敛 n=l n= 练习题：P3221；2；3；4;5

山东农业大学 高等数学 主讲人：苏本堂 例1. 若级数 均收敛 , 且 证明级数 收敛 . 证: n n n n 0  c − a  b − a (n =1, 2 , ), 则由题设 ( ) 1 n n  bn − a  = 收敛 ( ) 1 n n  c n − a  = 收敛 [( ) ] 1 n n n n =  c − a + a  = ( ) 1 n n =  c n − a  =   = + n 1 a n 收敛 练习题: P322 1 ; 2 ; 3 ; 4 ; 5

解答提示： P323题2.判别下列级数的敛散性 oncos 2n (2) (3) 3 ninn 2 n=12n n=1 0 00 (4) (a>0,s>0). n=1n 提示：(1).limn=1,所以 11 nn 因调和级数发散，据比较判别法的极限形式，原级数发散

山东农业大学 高等数学 主讲人：苏本堂 解答提示: P323 题2. 判别下列级数的敛散性: 提示: (1) lim =1, → n n  n 因调和级数发散, 据比较判别法的极限形式, 原级数发散 . 所以

y9 (2) 利用比值判别法，可知原级数发散， n=1 2n2 00 n cos2 uz 用比值法，可判断级数 收敛， (3) 3 n=1 2n 再由比较法可知原级数收敛， 1 (4) nn 因n充分大时10,s>0):用比值判别法可知： n=ins a1时发散 s>1时收敛； a=1时，与p级数比较可知 s≤1时发散

山东农业大学 高等数学 主讲人：苏本堂 利用比值判别法, 可知原级数发散. 用比值法, 可判断级数 因 n 充分大时 , ln 1 1 10 n n  ∴原级数发散 . : 2 cos (3) 1 3 2   n= n n n  (5) ( 0, 0): 1     = a s n a n s n 用比值判别法可知: 时收敛 ; 时, 与 p 级数比较可知 s 1 时收敛; 时发散. 再由比较法可知原级数收敛 . s 1 a 1 a 1 时发散. a =1 发散, 收敛

00 P323题3.设正项级数∑4n和∑yn都收敛，证明级数 n=1 n=1 ∑(un+yn)也收敛 n 提示：因lim un=limv=0,.存在W>0,当n>N时 n>0 N) 利用收敛级数的性质及比较判敛法易知结论正确

山东农业大学 高等数学 主讲人：苏本堂 P323 题3. 设正项级数 和 也收敛 . 提示: 因 lim = lim = 0 , → → n n n n u v 存在 N > 0, 又因 2( ) 2 2 n n  u + v 利用收敛级数的性质及比较判敛法易知结论正确. 都收敛, 证明级数 当n >N 时

本堂 P323题4.设级数∑n收敛，且1imn=1,问级数 n=1 n→0Un ∑ n是否也收敛？说明理由 n=1 提示：对正项级数，由比较判别法可知 ∑yn收敛， n=1 但对任意项级数却不一定收敛.例如，取 4,) Nn n n lim 1+lim (1) =1 n-→oln n-→oVn 00 级数∑4n收敛，级数∑yn发散 n=l n=l

山东农业大学 高等数学 主讲人：苏本堂 P323 题4. 设级数 收敛 , 且 是否也收敛？说明理由. 但对任意项级数却不一定收敛 . 问级数 提示: 对正项级数,由比较判别法可知 级数 收敛 , n n n u v → lim 收敛, 级数 发散 . n n n ( 1) 1 lim − = + → =1 例如, 取 n n v n n ( 1) 1 + − =

P323题5.讨论下列级数的绝对收敛性与条件收敛性： (1) (2) ∑(-1)*1sin. n=1 n=1 00 (3) (-1n+； (4) ∑（←1）n+10! n=1 n n=1 2h+l. 提示：(1)P>1时，绝对收敛， 0<p≤1时，条件收敛， psO时，发散 (2)因各项取绝对值后所得强级数 +1 收敛，故 n=1π 原级数绝对收敛

山东农业大学 高等数学 主讲人：苏本堂 ; 1 (3) ( 1) ln 1   = + − n n n n P323 题5.讨论下列级数的绝对收敛性与条件收敛性: ; sin (2) ( 1) 1 1 1 1   = + + + − n n n n   提示: (1) P >1 时, 绝对收敛 ; 0 < p ≤1 时, 条件收敛 ; p≤0 时, 发散 . (2) 因各项取绝对值后所得强级数 原级数绝对收敛 . , 故 1 1  1 收敛  = + n n 