《高等数学》课程教学资源（PPT课件，下册）对面积的曲面积分

山东农业大 主计 第四节对面积的曲面积分 一、对面积的曲面积分的概念与性质 二、对面积的曲面积分的计算法

山东农业大学 高等数学 主讲人：苏本堂 第四节 对面积的曲面积分 一、对面积的曲面积分的概念与性质 二、对面积的曲面积分的计算法

一、对面积的曲面积分的概念与性质 引例：设曲面形构件具有连续面密度P(x,y,2),求质 量M. 类似求平面薄板质量的思想，采用 (5k,7k,Sk) “大化小，常代变，近似和，求极限 的方法，可得 M-lim p(5e,m.5)ASe 2→0k=1 其中，入表示n小块曲面的直径的 最大值（曲面的直径为其上任意两点间距离的最大者）

山东农业大学 高等数学 主讲人：苏本堂 o x y z 一、对面积的曲面积分的概念与性质 引例: 设曲面形构件具有连续面密度 类似求平面薄板质量的思想, 采用 可得  = n k 1 M = ( , , )  k k  k 求质 “大化小, 常代变, 近似和, 求极限” 的方法,  量 M. 其中,  表示 n 小块曲面的直径的 最大值 (曲面的直径为其上任意两点间距离的最大者)

定义：设∑为光滑曲面，f(x,y)是定义在∑上的一 个有界函数，若对∑做任意分割和局部区域任意取点， “乘积和式极限” i2f(5,5)A记作 ∬faxy2ds k=1 都存在，则称此极限为函数f(x,yz)在曲面∑上对面积 的曲面积分或第一类曲面积分.其中f(化，y)叫做被积 函数，∑叫做积分曲面 据此定义，曲面形构件的质量为M=八p(x,y,2)dS 曲面面积为S=∬dS

山东农业大学 高等数学 主讲人：苏本堂 M (x, y,z)d S  =  定义: 设  为光滑曲面, “乘积和式极限” 都存在, 的曲面积分   f (x, y,z)d S 其中 f (x, y, z) 叫做被积 据此定义, 曲面形构件的质量为 曲面面积为 f (x, y, z) 是定义在  上的一 个有界函数, 记作 或第一类曲面积分. 若对  做任意分割和局部区域任意取点, 则称此极限为函数 f (x, y, z) 在曲面  上对面积 函数,  叫做积分曲面

对面积的曲面积分与对弧长的曲线积分性质类似 ·积分的存在性.若f(x,y,z)在光滑曲面∑上连续， 则对面积的曲面积分存在。 ·对积分域的可加性.若∑是分片光滑的，例如分成两 片光滑曲面∑1，∑2，则有 川2fx,y)ds=小2，fx,yz)ds+八5，fxa)ds ·线性性质.设k,k2为常数，则 小[kfx,y,2)±k28(x,y,z1S -6f,yds+儿eg0x)as

山东农业大学 高等数学 主讲人：苏本堂 则对面积的曲面积分存在. • 对积分域的可加性. , , 1 2 则有 =  f (x, y,z)d S 1 f (x, y,z)d S    k f (x, y,z)  k g(x, y,z) d S 1 2 • 线性性质.     = k f (x, y,z)dS  k g(x, y,z)dS 1 2 在光滑曲面  上连续, 对面积的曲面积分与对弧长的曲线积分性质类似. • 积分的存在性. 若  是分片光滑的, 例如分成两 片光滑曲面

二、对面积的曲面积分的计算法 定理：设有光滑曲面 Σ：z=z(x,y),(x,y)∈Dy f(化，y)在∑上连续，则曲面积分 八f(x,八，)dS存在，且有 八fx,y,)s (△Ok)xy (5k,k,Sk） =[pf,y.=()+z2(.)+z(x.y)dxdy 证明：由定义知 八2fa,y)ds=lm ∑f(5k,k,5)△S →0 k=1

山东农业大学 高等数学 主讲人：苏本堂 o x y z 定理: 设有光滑曲面 f (x, y, z) 在  上连续,  存在, 且有  f (x, y,z)dS  = Dx y f (x, y, ) 二、对面积的曲面积分的计算法 则曲面积分 证明: 由定义知  = n k 1 0 lim → Dxy ( , , )  k k  k k x y ( ) 

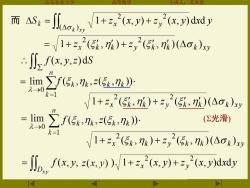
而△S=any1+,2(x,川+dd =1+2x2(5,7k)+zy2(5,k)(Aok)xy “J八fx,y,2)ds =2f5%,2》 k=1 V1+2x2(5k,)+2y2(5k,)(△ok)xy =]im∑f(5k,k,2(5,x)》 (光滑) k=1 √1+2x2(5,x)+3y2(5k,7k)(△ok)xy f(x,y.z(.y))+2(x)+,2(x.y)dxdy

山东农业大学 高等数学 主讲人：苏本堂 z x y z x y x y k x y x y 1 ( , ) ( , ) d d ( ) 2 2   + +  x k k y k k k xy 1 z ( , ) z ( , )( ) 2 2 = +   +    x k k y k k k xy 1 z ( , ) z ( , )( ) 2 2 +   +    x k k y k k k xy 1 z ( , ) z ( , )( ) 2 2 +   +    f x y z x y z x y x y x y Dx y ( , , ) 1 ( , ) ( , )d d 2 2 = + +  ( , , ( , )) k k k k f   z   ( , , ( , )) k k k k f   z     f (x, y,z)dS 而 (光滑)

山东农业大 化曲面积分为二重积分 设曲面Σ的方程为z=z(x,y),∑在xOy面上的投影区域 为D函数z=z(x,y)在D上具有连续偏导数，被积函数x, y,)在∑上连续，则 小fx,yaS=∬fxy2(x川W1+x+x,). 讨论： 如果积分曲面Σ由方程yW2,x)给出或由x=x0y,2)给 出，那么孔x,y,z)在∑上对面积的曲线面积分如何计算？ 提示： 对于2：y=(2,x),有 小fxy,2S=J∬fIx,(2,x,zV1+y2,x)+y2(2,x)dd

山东农业大学 高等数学 主讲人：苏本堂   = + +  Dzx z x f (x, y,z)dS f[x, y(z, x),z] 1 y (z, x) y (z,x)dzdx 2 2  化曲面积分为二重积分 设曲面的方程为z=z(x y) 在xOy面上的投影区域 为Dxy 函数z=z(x y)在Dxy上具有连续偏导数被积函数f(x y z)在上连续 则   = + +  Dx y x y f (x, y,z)dS f[x, y,z(x, y)] 1 z (x, y) z (x, y)dxdy 2 2  讨论 如果积分曲面由方程y=y(z x)给出或由x=x(y z)给 出 那么 f(x y z)在上对面积的曲线面积分如何计算? 提示 对于 y=y(z x) 有

化曲面积分为二重积分 要点：一代、二换、三投影 代：将曲面的方程代入被积函数 换：换面积元dS 投影：将曲面投影到坐标面得投影区域 注： (1)这里积分曲面的方程必须是单值显函数，否则 可利用可加性，分块计算，结果相加 (2)把曲面投影到哪一个坐标面，取决于曲面方程 即方程的表达形式 (3)将曲面的方程代入被积函数的目的和意义是 把被积函数化为二元函数

山东农业大学 高等数学 主讲人：苏本堂 化曲面积分为二重积分 要点：一代、二换、三投影 代：将曲面的方程代入被积函数 换：换面积元 dS 投影：将曲面投影到坐标面得投影区域 注： （1）这里积分曲面的方程必须是单值显函数，否则 可利用可加性，分块计算，结果相加 （2）把曲面投影到哪一个坐标面，取决于曲面方程 即方程的表达形式 （3）将曲面的方程代入被积函数的目的和意义是 把被积函数化为二元函数

例1.计算曲面积 分d,其中是球面2+y2+2 =a被平面z=h(0<h<a)截出的顶部 解：∑：z=Va2-x2-y2,(x,y)∈Dy Do:x2+y2sa2-h2 a 1++ 3=Ja-x-y -瓜心o rdr a2-r2 2aa n(a2alng

山东农业大学 高等数学 主讲人：苏本堂 Dxy 例1. 计算曲面积分 其中是球面 被平面 截出的顶部. 解: 2 2 2 2 Dxy : x + y  a − h 2 2 1 x y + z + z   z d S  =   2 0 a d 0 ln( ) 2 1 2 2 2 2 2 a h a a r +   − −   =   − − = Dx y a x y a x y 2 2 2 d d  − − 2 2 0 2 2 a h d a r r r o x z y  h a

例2.计算∬yzdS,其中Σ是由平面x+y+z=1与 坐标面所围成的四面体的表面： 解：设∑1，∑2，∑3，∑4分别表示∑在平面 x=0,y=0,z=0,x+y+z=1上的部分，则 原式+儿，+儿，+)xwy:as公 川2 xy-dS 24=1-x-ykw=n,062 =5可6d61-x-Wdy=3%20

山东农业大学 高等数学 主讲人：苏本堂 例2. 计算 其中 是由平面 坐标面所围成的四面体的表面. o z y x 1 1 1 解: 设 上的部分, 则 1 2 3 4  ,  ,  ,      = 4 xyz d S : 1 , 4  z = − x − y        −  0 1 0 1 ( , ) : x y x x y Dxy  − − − x y x y y 1 0 (1 ) d 120 3 = 与  = 1 0 3 x dx         + + + 1 2 3 4  xyz dS  原式  = 分别表示 在平面