《高等数学》课程教学资源（PPT课件，下册）重积分的应用

东液大 第四节 重积分的应用 一、立体体积 二、曲面的面积 三、物体的质心 四、转动惯量 五、引力

山东农业大学 高等数学 主讲人：苏本堂 第四节 重积分的应用 一、立体体积 二、曲面的面积 三、物体的质心 四、转动惯量 五、引力

方本 1.能用重积分解决的实际问题的特点 分布在有界闭域上的整体量 所求量是 对区域具有可加性 2.用重积分解决问题的方法 ·用微元分析法（元素法） ·从积分定义出发建立积分式 3.解题要点 画出积分域、选择坐标系、确定积分序、 定出积分限、计算要简便

山东农业大学 高等数学 主讲人：苏本堂 1. 能用重积分解决的实际问题的特点 所求量是 对区域具有可加性 • 从积分定义出发 建立积分式 • 用微元分析法 (元素法) 分布在有界闭域上的整体量 3. 解题要点 画出积分域、选择坐标系、确定积分序、 定出积分限、计算要简便 2. 用重积分解决问题的方法

东农 一、立体体积 ·曲顶柱体的顶为连续曲面z=f(x,y),(x,y)∈D, 则其体积为 V=j∬nfox,drd ·占有空间有界域Ω的立体的体积为 V=j川dxdyd-

山东农业大学 高等数学 主讲人：苏本堂 一、立体体积 • 曲顶柱体的顶为连续曲面 则其体积为  = D V f (x, y)dxdy • 占有空间有界域  的立体的体积为  V = dxdydz

山东农业才 方本 例1计算由曲面z=1-4x2-y2 与x0y面所围成的立体的体积 解一用二重积分D:4x2+y2≤1 V=J∬-4x2-y2)k 由对称性得 D V=4∬0-4x2 广=4a (1-4x2-y2)d D 解==亚==了奇了k V1-4x21-4x2-y

山东农业大学 高等数学 主讲人：苏本堂 计算由曲面 2 2 z = 1− 4x − y 解一 用二重积分 与 xoy 面所围成的立体的体积 : 4 1 2 2 D x + y   = − − D V (1 4x y )dxdy 2 2 由对称性得 例1    − = − − = − − 1 2 1 4 0 2 2 2 1 0 2 2 4 (1 4 ) 4 (1 4 ) D x V x y dxdy dx x y dy 1 3 2 4 2 2 2 0 0 8 8 1 (1 4 ) cos 3 3 2 4 x dx tdt   = − =  =   解二   = =  1 V dv 4 dv    − − − = = 2 1 0 1 4 0 1 4 0 2 2 2 4 4 x x y dx dy dz 

例2求z=2-x2-y,z=x2+y2所围成的立体的体积 解-V=-=∬2-x2-y)o-∬x2+y)do =2∬1-x2-y2)do （用极坐标) 2jaj-r内= 2 解二 2 是柱形区域，用柱坐标 L 2-1 v=∬w=了ao =2πr(2-2r2)dr=元

山东农业大学 高等数学 主讲人：苏本堂 所围成的立体的体积 2 2 2 2 求 z = 2 − x − y ,z = x + y 解一   = − = − − − + D D V V V (2 x y )d (x y )d 2 2 2 2 2 1  = − − D 2 (1 x y )d 2 2 （用极坐标）   = − =    2 0 1 0 2 2 d (1 r )rdr 解二  是柱形区域，用柱坐标  =  V dv    − =   2 0 1 0 2 2 2 r r d dr rdz  = − = 1 0 2 2 r(2 2r )dr  例2

山东农业大 方本堂 二、曲面的面积 设光滑曲面S:z=f(x,y),(x,y)∈D 则面积A可看成曲面上各点M(x,y,z) 处小切平面的面积dA无限积累而成！ 设它在D上的投影为do,则 doy do=cosy.d4 1+fx2(x,)+f2(x,y) dA=1+f2(x,y)+fy2(x,y)do (称为面积元素)

山东农业大学 高等数学 主讲人：苏本堂  M d A z d n 二、曲面的面积 x y z S o 设光滑曲面 则面积 A 可看成曲面上各点 M (x, y,z) 处小切平面的面积 d A 无限积累而成. 设它在 D 上的投影为 d , d = cos d A 1 ( , ) ( , ) 1 cos 2 2 f x y f x y + x + y  = d 1 ( , ) ( , ) d 2 2 A f x y f x y = + x + y (称为面积元素) 则   M n  d

故有曲面面积公式 A=1+2(x.y)+f2(x.y)da 即 4n1+2+导axdy 若光滑曲面方程为x=g(y,z),(y,)∈Dy:,则有 D 1) 若光滑曲面方程为y=h(2,x),(z,x)∈Dx,则有 4=川++dd

山东农业大学 高等数学 主讲人：苏本堂 故有曲面面积公式 1 ( , ) ( , ) d 2 2  = + + D x y A f x y f x y x y y z x z A D 1 ( ) ( ) d d 2 2    +   = + 若光滑曲面方程为 ( , ) , ( , ) , Dy z x = g y z y z  则有 Dy z 即 z x x y z y A 1 ( ) ( ) d d 2 2   +   = +  若光滑曲面方程为 ( , ) , ( , ) , Dz x y = h z x z x  则有

例3求半径为R的球的表面积. 解球面的面积A为上半球面面积的两倍， 球心在原点的上半球面的方程为z=√R2-x2-y2,而 -x -y OxR2-x0R2-x22 所以 12+象+ x2+y2≤R 2胶-2a rdr =-4πRVR2-r2|8=4πR2. 反常积分

山东农业大学 高等数学 主讲人：苏本堂 解 球面的面积A为上半球面面积的两倍 例3 求半径为R的球的表面积 2 2 2 R x y x x z − − − =    2 2 2 R x y y y z − − − =    2 2 2 R x y x x z − − − =    2 2 2 R x y y y z − − − =    所以 2 2 2 1 ( ) ( ) 2 2 2 y z x z A x y R   +   = +  +  dxdy R x y R x y R 2 2 2 2 2 2 2 − − =  +    − =      2 0 0 2 2 2 R R d R d 球心在原点的上半球面的方程为 2 2 2 z= R − x − y  而 2 0 2 2 4 R R 4 R R =−  − =   2 0 0 2 2 2 R rdr R d R r  =  −   2 2 0 4 R = − − R R r

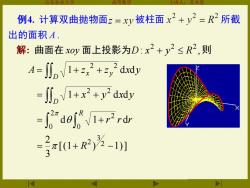
例4.计算双曲抛物面z=xy被柱面x2+y2=R2所截 出的面积A. 解：曲面在x0y面上投影为D:x2+y2≤R2,则 A=川nN1+z2+,2ddy =j川nV1+x2+y2dxd -dord 3a1+R2)为-1)1

山东农业大学 高等数学 主讲人：苏本堂 例4. 计算双曲抛物面 被柱面 所截 解: 曲面在 xoy 面上投影为 : , 2 2 2 D x + y  R 则 A z z x y D x y 1 d d 2 2  = + + x y x y D 1 d d 2 2  = + + r r r R d 1 d 0 2 2 0   = +   [(1 ) 1)] 3 2 2 3 2 =  + R − 出的面积 A

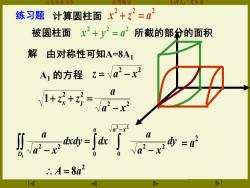
山东农业大 高等数学 练习题计算圆柱面x2+z2=2 被圆柱面x2+y2=2所截的部分的面积 解由对称性可知A=8A1 A1的方程z=V2-x2 1++ -Na-x 。”e了o”4=d /a2 ∴A=8a2

山东农业大学 高等数学 主讲人：苏本堂 计算圆柱面 2 2 2 x + z = a 被圆柱面 x 2 + y 2 = a 2 所截的部分的面积 解 由对称性可知A=8A1 A1 的方程 2 2 z = a − x 2 2 2 2 1 a x a z z x y − + + =    − − = − 1 2 2 0 0 2 2 2 2 D a a x dy a x a dxdy dx a x a 2 = a 2  A = 8a 练习题