《高等数学》课程教学资源（PPT课件，下册）曲面及其方程

§8.5曲面及其方程 一、曲面研究的基本问题 二、旋转曲面 三、柱面 四、二次曲面 网

山东农业大学 高等数学 主讲人：苏本堂 一、曲面研究的基本问题 二、旋转曲面 三、柱面 §8.5 曲面及其方程 四、二次曲面

主 苏本堂 一、曲面研究的两个基本问题 (1)已知一曲面作为点的几何轨迹时，建立这曲面的 方程； (2)已知坐标x、y和z间的一个方程时，研究这方程所 表示的曲面的形状

山东农业大学 高等数学 主讲人：苏本堂 (1) 已知一曲面作为点的几何轨迹时, 建立这曲面的 方程; (2) 已知坐标x、y和z间的一个方程时, 研究这方程所 表示的曲面的形状. 一、曲面研究的两个基本问题

例1.求动点到定点Mo(xo,yo,z0)距离为R的轨迹 方程 解：设轨迹上动点为M(x,y,z),依题意MoM=R 即 V(x-x)2+(y-0)2+(2-20)2=R 故所求方程为 (x-0)2+(y-0)2+(2-20)2=R2 特别，当M在原点时，球面方程为 Mo x2+y2+22=R2 2=±√R2-x2-y2表示上（下）球面

山东农业大学 高等数学 主讲人：苏本堂 故所求方程为 例1. 求动点到定点 方程. 特别,当M0在原点时,球面方程为 解: 设轨迹上动点为 即 依题意 距离为 R 的轨迹 x y z o M M0 表示上(下)球面 . x − x + y − y + z − z = R 2 0 2 0 2 0 ( ) ( ) ( ) 2 2 0 2 0 2 0 (x − x ) + ( y − y ) + (z − z ) = R 2 2 2 2 x + y + z = R

山东农业大 主讲 方本堂 例设有点A(1,2,3)和B(2,-1,4),求线段AB的垂直平 分面的方程 解由题意知道，所求的平面就是与A和B等距离的点 的几何轨迹， 设Mx,y,)为所求平面上的任一点，则有 AM-BM, 即 Vx-1)2+y-2)2+2-3)2=Vx-2)2+y+102+(z-4)2 等式两边平方，然后化简得 2x-6y+2z-7=0 这就是所求的平面的方程

山东农业大学 高等数学 主讲人：苏本堂 例 设有点A(1, 2, 3)和B(2, −1, 4), 求线段AB的垂直平 分面的方程. 由题意知道, 所求的平面就是与A和B等距离的点 的几何轨迹. 设M(x, y, z)为所求平面上的任一点, 则有 |AM|=|BM|, 等式两边平方, 然后化简得 2x−6y+2z−7=0. 这就是所求的平面的方程. 解 即 2 2 2 2 2 2 (x−1) +(y−2) +(z−3) = (x−2) +(y+1) +(z−4) 

例3方程x2+y2+z2-2x+4y=0表示怎样的曲面？ 解通过配方，原方程可以改写成 (x-1)2+0y+2)2+z2=5. 这是一个球面方程，球心在点ML,-2,0)、半径为R=V5 一般地，三元二次方程 Ax2+Ay2+A22+Dx+Ey+Fz+G=0 的图形就是一个球面

山东农业大学 高等数学 主讲人：苏本堂 例3 方程x 2+y 2+z 2−2x+4y=0表示怎样的曲面？ 解 通过配方, 原方程可以改写成 (x−1) 2+(y+2) 2+z 2=5. 这是一个球面方程 球心在点 (1, 2, 0) M 0 − 、半径为 R= 5  一般地, 三元二次方程 Ax2+Ay2+Az2+Dx+Ey+Fz+G=0 的图形就是一个球面

导效 主 方本 二、旋转曲面 定义2.一条平面曲线绕其平面上一条定直线旋转 周所形成的曲面叫做旋转曲面.该定直线称为旋转 轴. 例如：

山东农业大学 高等数学 主讲人：苏本堂 定义2.一条平面曲线 二、旋转曲面 绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面. 该定直线称为旋转 轴 . 例如 :

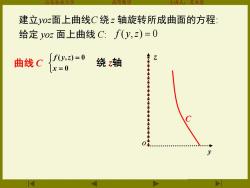
建立y0z面上曲线C绕z轴旋转所成曲面的方程 给定y0z面上曲线C:f(y,z)=0 曲线C 绕z轴

山东农业大学 高等数学 主讲人：苏本堂 建立yoz面上曲线C 绕 z 轴旋转所成曲面的方程: 给定 yoz 面上曲线 C: f ( y,z) = 0 曲线 C    = = 0 ( , ) 0 x f y z C y z o 绕 z轴

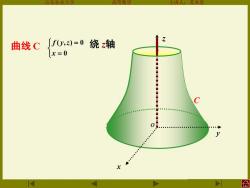
山东农业大雪 主讲人：本堂 曲线C ∫f,)=0绕轴 x=0 合

山东农业大学 高等数学 主讲人：苏本堂 曲线 C    = = 0 ( , ) 0 x f y z x C y z o 绕 z轴

曲线C ∫fy,)=0绕轴 x=0 旋转一周得旋转曲面S N0,y1,z1) M HMc,z)∈S f0y,)0 乙 Z 乙1=Z lyFMP=x2+y2

山东农业大学 高等数学 主讲人：苏本堂 曲线 C    = = 0 ( , ) 0 x f y z 旋转一周得旋转曲面 S S C M N (0, , ) 1 1 y z  z = z 1 z P | y1 |= MP 1 y 1 z y z o 绕 z轴 . 2 2 = x + y f (y1, z1 )=0 M(x,y,z) . x  S

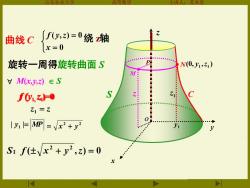
主讲人 苏本堂 曲线C 「f(y,)=0绕轴 x=0 旋转一周得旋转曲面S P N(0,y1,z1) M VMcJ,z)∈S f(y.4 乙1=Z 0 ly,FMP=x2+y2 y S:f±Vx2+y2,z)=0

山东农业大学 高等数学 主讲人：苏本堂 曲线 C    = = 0 ( , ) 0 x f y z 旋转一周得旋转曲面 S x S C M N (0, , ) 1 1 y z z = z 1 z P | y1 |= MP 1 y 1 z ( , ) 0 2 2 S：f  x + y z = . 绕 z轴 . . 2 2 = x + y  f (y1, z1 )=0 M(x,y,z) f (y1, z1 f (y1 )=0 , z1 )=0 . y z o  S