《高等数学》课程教学资源（PPT课件，上册）微积分基本公式

主 第二节 微积分基本公式 一、引例 二、积分上限的函数及其导数 三、牛顿一莱布尼茨公式

山东农业大学 高等数学 主讲人：苏本堂 第二节 微积分基本公式 三、牛顿—莱布尼茨公式 一、引例 二、积分上限的函数及其导数

引例 设物体从某定点开始作直线运动，在时刻物体所经 过的路程为S(),速度为v=v(t)=S(t)(v(t)≥0)，则在时间间隔 [T,T,]内物体所经过的路程S可表示为 ST)-ST)及0d, 即 d=S)-SG). 上式表明，速度函数v()在区间[T,T]上的定积分等 于()的原函数S(t)在区间[T,T]上的增量 这个特殊问题中得出的关系是否具有普遍意义呢？

山东农业大学 高等数学 主讲人：苏本堂 设物体从某定点开始作直线运动, 在t时刻物体所经 过的路程为S(t), 速度为v=v(t)=S(t)(v(t)0), 则在时间间隔 [T1 , T2 ]内物体所经过的路程S可表示为 上式表明, 速度函数v(t)在区间[T1 , T2 ]上的定积分等 于v(t)的原函数S(t)在区间[T1 , T2 ]上的增量. 这个特殊问题中得出的关系是否具有普遍意义呢？ ( ) ( ) S T2 −S T1 及 v t dt T T ( ) 2 1   即 ( ) ( ) ( ) 2 1 2 1 v t dt S T S T T T = −  即  一、引例

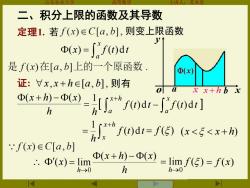
等数 二、积分上限的函数及其导数 定理1.若f(x)∈C[a,b],则变上限函数 Φ(x)=∫f)dt 是f(x)在[a,b]上的一个原函数 Φ() 证：x,x+h∈[a,b],则有 xx+hb x x+w-f0d-0] h 打f@a=f5(<E<x+分 .'f(x)∈C[a,b] ∴.Φ'(x)=lim Φ(x+h)-Φ(x) 2 =limf()=f(x) h-→0 h h-→0

山东农业大学 高等数学 主讲人：苏本堂 二、积分上限的函数及其导数 则变上限函数   = x a (x) f (t)dt 证: x, x + h[a, b], 则有 h (x + h) −(x)  h 1 =    − + x a x h a f (t)dt f (t)dt  + = x h x f t t h ( )d 1 = f () (x   x + h) h x h x h ( ) ( ) lim 0  + − = → lim ( ) 0 f  h→  (x) = = f (x) 定理1. 若 a b x y o x + h (x) x

注： 1)定理1证明了连续函数的原函数是存在的.同时为 通过原函数计算定积分开辟了道路. 2)变限积分求导&」/0)dr-fa侧 品foar-imwp四 dlod-+。ona =f[p(x)]p'(x)-f[w(x)]W(x)

山东农业大学 高等数学 主讲人：苏本堂 注: 1) 定理 1 证明了连续函数的原函数是存在的. 2) 变限积分求导:  ( ) ( )d d d x a f t t x  = f [(x)](x) 同时为 通过原函数计算定积分开辟了道路 .  ( ) ( ) ( )d d d x x f t t x   = f [(x)](x) − f [(x)](x)   +   =   ( ) ( ) ( )d ( )d d d x a a x f t t f t t x  

主计 方本 例1.求lim x→0 x2 2 解：原式 -limeco.(←sin) x→0 2x 2e 例2.确定常数a,b,c的值，使 ax-sinx lim =c(c≠0) d+2)d 解：：x→0时，ax-sinx→0，c≠0，.b=0. 原式=lim a-cosx a-cosx lim =C x0ln(1+x2) c0,故a=1.又由1-c0sxx2,得c=2:

山东农业大学 高等数学 主讲人：苏本堂 ( sin ) 2 cos e x x  − − 例1. 求 解: 原式 0 lim → = − x 2x 2e 1 = 例2. 确定常数 a , b , c 的值, 使 解:  b = 0. 原式 = c ≠0 , 故 a =1. 又由 ～ , 得 . 2 1 c =

例3设fx)在[0，+o)内连续且x)>0.证明函数 F(x)= 5fo0h 5foadn 在(0，+∞)内为单调增加函数. 证明因为 r(a-feffad f(x(x-t)f(t)dt (d (f0)d2 按假设，当00,(x-)f()>0,所以 f(Odt-0,(x-D)f(Odi-0, 从而F'(x)>0(x>0),因此F(x)在(0，+o)内为单调增加函数

山东农业大学 高等数学 主讲人：苏本堂 例3 设f(x)在[0, +)内连续且f(x)>0 证明函数   = x x f t dt tf t dt F x 0 0 ( ) ( ) ( ) 在(0 +)内为单调增加函数 证明因为 2 0 0 0 ( ( ) ) ( ) ( ) ( ) ( ) ( )    −  = x x x f t dt xf x f t dt f x tf t dt F x 2 0 0 ( ( ) ) ( ) ( ) ( )   − = x x f t dt f x x t f t dt  2 0 0 0 ( ( ) ) ( ) ( ) ( ) ( ) ( )    −  = x x x f t dt xf x f t dt f x tf t dt F x 2 0 0 ( ( ) ) ( ) ( ) ( )   − = x x f t dt f x x t f t dt  按假设 当0tx时f (t)>0 (x−t)f (t)>0 所以 ( ) 0 0   f t dt x  ( ) ( ) 0 0 −   x t f t dt x ( ) 0  0   f t dt x  ( ) ( ) 0 0 −   x t f t dt x  从而F (x)>0(x>0) 因此F(x)在(0 +)内为单调增加函数

山东农业大 主计 办本堂 三、牛顿一莱布尼茨公式 定理3（牛顿-一莱布尼茨公式） 若F(x)是连续函数x)在区间[a,b]上的一个原函数， 则 f(x)dx-F(6b)-F(a). 证明 由于()=fd)dt也是人x)的原函数 因为Fx)和Φ(x)都是x)的原函数，所以存在常数C,使 F(x)-D(x)=C. 由F(a)-Φ(a=C及D(a=0,得C=Fa),Fx)-Φ(x)=F(a 由Fb)-Φ(b)=Fa),得Φ(b)=Fb)F(a,即 [f(x)d=F(b)-F(d)

山东农业大学 高等数学 主讲人：苏本堂 若F(x)是连续函数f(x)在区间[a, b]上的一个原函数, 则 f (x)dx F(b) F(a) b a = −   定理3(牛顿−−莱布尼茨公式) f (x)dx F(b) F(a) b a = −   证明 因为F(x)和(x)都是f(x)的原函数 所以存在常数C 使 F(x)−(x)=C. 由F(a)−(a)=C及(a)=0, 得C=F(a), F(x)−(x)=F(a). 由F(b)−(b)=F(a), 得(b)=F(b)−F(a), 即 由于  =  也是f(x)的原函数 x a (x) f (t)dt 三、牛顿—莱布尼茨公式

例4.计算11+ 3 dx 解 1√3 arctan√3-arctan(-l) = 7 -元 例5.计算正弦曲线y=sinx在[0，π]上与x轴所围成 的面积 yy=sinx 解：A=∫0 sinxdx =-COSx 6-1-1川=26 πx

山东农业大学 高等数学 主讲人：苏本堂 例4. 计算 解: x x x arctan 1 3 d 1 2 = + − 1 3 − = arctan 3 − arctan(−1) 3  =  12 7 = 例5. 计算正弦曲线 的面积 . 解:  =  0 A sin xdx = −cos x 0  = −[−1−1] = 2 ) 4 (  − − y o x y = sin x 

主 本堂 例6求，max{x,x2c. 解 由图形可知 f(x)=max{x,x2 y=x x2-2≤x≤0 = 0≤x≤1， x2 1≤x≤2 原式-+小+x=

山东农业大学 高等数学 主讲人：苏本堂 例6 求 max{ , } . 2 2 2 − x x dx 解 由图形可知 ( ) max{ , } 2 f x = x x , 1 2 0 1 2 0 2 2          −   = x x x x x x     = + + − 2 1 2 1 0 0 2 2 原式 x dx xdx x dx . 2 11 = x y o 2 y = x y = x − 2 1 2

例7汽车以每小时36km速度行驶，到某处需要减 速停车.设汽车以等加速度a=-5m/s2刹车.问从开始 刹车到停车，汽车走了多少距离？ 解汽车刹车时的初速度为 %=36km/h=36x1000 m/s=10m/s. 3600 刹车后t时刻汽车的速度为 v(t)=Vo+at=10-5t. 当汽车停止时，有 v(t0)=10-5t=0,t仁2(S) 于是从开始刹车到停车汽车所走过的距离为 s=0ah=0-5dt=[l0-5fP6=10(m

山东农业大学 高等数学 主讲人：苏本堂 例7 汽车以每小时36km速度行驶, 到某处需要减 速停车.设汽车以等加速度a=−5m/s2刹车. 问从开始 刹车到停车,汽车走了多少距离？ 于是从开始刹车到停车汽车所走过的距离为 t=2(s). 当汽车停止时, 有 v(t)=v0+at=10−5t. 刹车后 t 时刻汽车的速度为 v(t)=10−5t =0, 解 汽车刹车时的初速度为 m/s 10m/s 3600 36 1000 0 36km/h =  v = =  s v(t)dt (10 5t)dt 2 0 2 0 = = −   ] 10 (m) 2 1 [10 5 2 0 2 s v(t)dt (10 5t)dt = t−  t =  2 0 2 0 = = −   ] 10 (m) 2 1 [10 5 2 0 2 s v(t)dt (10 5t)dt = t−  t =  2 0 2 0 = = −   ] 10 (m) 2 1 [10 5 2 0 2 = t−  t = 