《高等数学》课程教学资源（PPT课件，上册）函数的连续性

第八节函数的连续性 函数连续性的定义 二、函数的间断点

山东农业大学 高等数学 主讲人：苏本堂 第八节函数的连续性 一、 函数连续性的定义 二、函数的间断点

一、函数连续性的定义 定义：设函数y=f(x)在xo的某邻域内有定义，且 limf(x)=f(x),则称函数f(x)在x连续 x→x0 可见，函数∫(x)在点x0连续必须具备下列条件： (I)f(x)在点xo有定义，即f(xo)存在， (2)极限limf(x)存在， X→x0 (3) lim f(x)=f(xo). x→X0

山东农业大学 高等数学 主讲人：苏本堂 可见 , 函数 在点 0 x 一、 函数连续性的定义 定义: 在 的某邻域内有定义 , 则称函数 ( ) . f x 在x0 连续 (1) 在点 即 (2) 极限 (3) 设函数 连续必须具备下列条件: 存在 ; 且 有定义 , 存在 ;

若f(x)在某区间上每一点都连续，则称它在该区间上 连续，或称它为该区间上的连续函数. 在闭区间[a,b]上的连续函数的集合记作C[a,b] 例如，P(x)=a0+a4x+.+anx” (有理整函数) 在(-0，+0)上连续 又如，有理分式函数R()= P(x) 2(x) 在其定义域内连续 只要Q(x)≠0，都有limR(x)=R(xo) x→x0

山东农业大学 高等数学 主讲人：苏本堂 ( , ), lim ( ) ( ) continue 0 0 0 x P x P x x x   − +  = → 若 在某区间上每一点都连续 , 则称它在该区间上 连续 , 或称它为该区间上的连续函数 . C[a, b]. 例如, 在 上连续 . ( 有理整函数 ) 又如, 有理分式函数 在其定义域内连续. 在闭区间 上的连续函数的集合记作 只要 ( ) 0, Q x0  都有 lim ( ) ( ) 0 0 R x R x x x = →

1东 对自变量的增量△r=x-xo,有函数的增量 △y=f(x)-f(xo)=f(xo+△)-f(xo) 函数f(x)在点x,连续有下列等价命题： lim f(x)=f(xo)-lim f(xo+Ax)=f(xo) x→x0 lim△y=0 tyy=f(x) △x-→0 f(xo)=f(xo)=f(xo") △x 左连续 右连续 Xo xx ε>0,6>0，当x-x=△x<6时，有 f(x)-f(x)=△y<8

山东农业大学 高等数学 主讲人：苏本堂 对自变量的增量 有函数的增量 y = f (x) o x y 0 x x x y lim ( ) ( ) 0 0 f x f x x x = → lim ( ) ( ) 0 0 0 f x x f x x +  =  → lim 0 0  =  → y x ( ) ( ) ( ) 0 0 0 − + f x = f x = f x 左连续 右连续   0,   0, 当 x − x0 = x   时, 有 f (x) − f (x ) = y   0 函数 在点 连续有下列等价命题:

例.证明函数y=sinx在(-0，+oo)内连续 证：x∈(-0，+0) △y=sin(x+△x)-sinx=2 sincos(x+) Ay=2 sin cos(x+) ≤21=Ax→00 即 lim△y=0 △x→0 这说明y=sinx在(-o,+oo)内连续 同样可证：函数y=c0sx在(-o0,+o0)内连续

山东农业大学 高等数学 主讲人：苏本堂 例. 证明函数 在 内连续 . 证: x(−, + ) y = sin(x + x) −sin x 2 sin cos( ) 2 2 x x y x    = + = x x → 0 即 这说明 在 内连续 . 同样可证: 函数 在 内连续 . 0

山东农业大 二、函数的间断点 设f(x)在点x。的某去心邻域内有定义，则下列情形 之一函数f(x)在点x不连续： (I)函数f(x)在x无定义； (2)函数f(x)在x。虽有定义，但imf(x)不存在； x→X0 (3)函数f(x)在x虽有定义，且mf(x)存在，但 x→xo limf(x)≠f(xo) x→X0 这样的点x。称为间断点

山东农业大学 高等数学 主讲人：苏本堂 在 在 二、 函数的间断点 (1) 函数 (2) 函数 不存在; (3) 函数 存在 , 但 lim ( ) ( ) 0 0 f x f x x x  → 不连续 : 设 在点 的某去心邻域内有定义 , 则下列情形 这样的点 之一函数 f (x) 在点 虽有定义 , 但 虽有定义 , 且 称为间断点. 在 无定义 ;

间断点分类： 第一类间断点： f(x)及f(x,)均存在， 若f(x)=f(x,),称x,为可去间断点 若f(x)≠f(x,),称为跳跃间断点 第二类间断点： f(x)及(x)中至少一个不存在， 若其中有一个为o0,称x,为无穷间断点 若其中有一个为振荡，称X,为振荡间断点

山东农业大学 高等数学 主讲人：苏本堂 间断点分类: 第一类间断点: 及 均存在 , 若 称 0 x 若 称 0 x 第二类间断点: 及 中至少一个不存在 , 称 0 x 若其中有一个为振荡 , 称 0 x 若其中有一个为 , 为可去间断点. 为跳跃间断点. 为无穷间断点 . 为振荡间断点

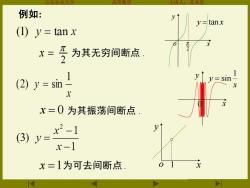
山东农业大 主讲 苏本堂 例如： y=tanx (I①)y=tanx X三 为其无穷间断点 (2) y=sin x x=0为其振荡间断点. x2-1 1 (3)y= x-1 x=1为可去间断点

山东农业大学 高等数学 主讲人：苏本堂 2  x = 为其无穷间断点 . x = 0 为其振荡间断点 . x =1为可去间断点. o x y 1 例如: y = tan x 2  x y o x y x y 1 = sin 0

x,x≠1 (4)y=f(x)= y x=1 11= 显然limf(x)=1≠f(I) x->l x=1为其可去间断点 x-1,x0 f(0)=-1, f(0*)=1 x=O为其跳跃间断点

山东农业大学 高等数学 主讲人：苏本堂 1 lim ( ) 1 (1) 1 f x f x =  → 显然 x =1 为其可去间断点 .    =  = = , 1 , 1 ( ) 2 1 x x x (4) y f x o x y 2 1 1 (5)     +  = −  = = 1 , 0 0 , 0 1 , 0 ( ) x x x x x y f x x y o 1 −1 (0 ) = −1, − f (0 ) =1 + f x = 0 为其跳跃间断点

山东很 主计 方本草 内容小结 1.f(x)在点x连续的等价形式 limf(x)=f(xo)三lim[f(xo+△r)-f(xo)】=0 x→x0 Ax→0 f(xo)=f(xo)=f(xo) 左连续 右连续 2.f(x)在点xo间断的类型 可去间断点 第一类间断点 跳跃间断点 左右极限都存在 无穷间断点) 左右极限至少有一 第二类间断点 振荡间断点 个不存在

山东农业大学 高等数学 主讲人：苏本堂 内容小结 左连续 右连续 第一类间断点 可去间断点 跳跃间断点 左右极限都存在 第二类间断点 无穷间断点 振荡间断点 左右极限至少有一 个不存在 在点 间断的类型 在点 连续的等价形式