《高等数学》课程教学资源（PPT课件）第八章_D8_5曲面方程

第五节 第八章 曲面及其方程 一、 曲面方程的概念 二、旋转曲面 三、 柱面 四、二次曲面 HIGH EDUCATION PRESS 机动目录上页下页返回结束

四、二次曲面 第五节 一、曲面方程的概念 二、旋转曲面 三、柱面 机动 目录 上页 下页 返回 结束 曲面及其方程 第八章

曲面方程的概念 引例：求到两定点4(1,2,3)和B(2,-1,4)等距离的点的 轨迹方程 解：设轨迹上的动点为M(x,y,z),则AM=BM,即 V(x-1)2+(y-2)2+(e-3)2 =(x-2)2+(y+1)2+(z-4) 化简得 2x-6y+2z-7=0 说明：动点轨迹为线段AB的垂直平分面！ 显然在此平面上的点的坐标都满足此方程 不在此平面上的点的坐标不满足此方程， HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、曲面方程的概念 求到两定点A(1,2,3) 和B(2,-1,4)等距离的点的 2 2 2 (x −1) + (y − 2) + (z − 3) 化简得 2x − 6y + 2z − 7 = 0 即 说明: 动点轨迹为线段 AB 的垂直平分面. 引例: 显然在此平面上的点的坐标都满足此方程, 不在此平面上的点的坐标不满足此方程. 2 2 2 = (x − 2) + ( y +1) + (z − 4) 解:设轨迹上的动点为 M (x, y,z),则 AM = BM , 轨迹方程. 机动 目录 上页 下页 返回 结束

定义1.如果曲面S与方程F(x,yz)=0有下述关系 (1)曲面S上的任意点的坐标都满足此方程， (2)不在曲面S上的点的坐标不满足此方程 则F(x,yz)=0叫做曲面S的方程 F(x,y,2)=0 曲面S叫做方程F(x,yz)=0的图形 两个基本问题： (1)已知一曲面作为点的几何轨迹时 求曲面方程 (2) 已知方程时，研究它所表示的几何形状 (必要时需作图) HIGH EDUCATION PRESS 机动目录上页下页返回结束

定义1. F(x, y,z) = 0 S z y x o 如果曲面 S 与方程 F( x, y, z ) = 0 有下述关系: (1) 曲面 S 上的任意点的坐标都满足此方程; 则 F( x, y, z ) = 0 叫做曲面 S 的方程, 曲面 S 叫做方程 F( x, y, z ) = 0 的图形. 两个基本问题 : (1) 已知一曲面作为点的几何轨迹时, (2) 不在曲面 S 上的点的坐标不满足此方程, 求曲面方程. (2) 已知方程时 , 研究它所表示的几何形状 ( 必要时需作图 ). 机动 目录 上页 下页 返回 结束

例1.求动点到定点M0(xo,yo,z0)距离为R的轨迹 方程 解：设轨迹上动点为M(x,y,z),依题意MoM=R 即 V(x-xo)2+(0y-0)2+(2-202=R 故所求方程为 (x-x)2+y-%)2+(E-o)2=R2 特别，当M在原点时球面方程为 x2+y2+z2=R2 2=±√R2-x2-y2表示上（下球面 HIGH EDUCATION PRESS 是上页下页返回结束

故所求方程为 例1. 求动点到定点 方程. 特别,当M0在原点时,球面方程为 解: 设轨迹上动点为 即 依题意 距离为 R 的轨迹 x y z o M M0 表示上(下)球面 . x − x + y − y + z − z = R 2 0 2 0 2 0 ( ) ( ) ( ) 2 2 0 2 0 2 0 (x − x ) + (y − y ) + (z − z ) = R 2 2 2 2 x + y + z = R 机动 目录 上页 下页 返回 结束

例2.研究方程x2+y2+z2-2x+4y=0表示怎样 的曲面 解：配方得 (x-1)2+(0y+2)2+z2=5 此方程表示 球心为M(1,-2,0), 半径为√5的球面. 说明：如下形式的三元二次方程(A≠0) 4Ax2+y2+z2)+Dx++F2+G=0 都可通过配方研究它的图形.其图形可能是 一个球面，或点，或虚轨迹 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例2. 研究方程 解: 配方得 5 (1, 2, 0), 此方程表示: M0 − 说明: 如下形式的三元二次方程 ( A≠ 0 ) 都可通过配方研究它的图形. 其图形可能是 的曲面. 表示怎样 半径为 的球面. 球心为 一个球面 , 或点 , 或虚轨迹. 机动 目录 上页 下页 返回 结束

二、旋转曲面 定义2.一条平面曲线绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面.该定直线称为旋转 轴· 例如： HIGH EDUCATION PRESS 机动目录上页下页返回结束

定义2. 一条平面曲线 二、旋转曲面 绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面. 该定直线称为旋转 轴 . 例如 : 机动 目录 上页 下页 返回 结束

建立voz面上曲线C绕z轴旋转所成曲面的方程： 给定y0z面上曲线C:f(y,z)=0 若点M,(0,)∈C,则有 f(1,)=0 当绕z轴旋转时，该点转到 M(0,y1,2） M(x/y,=) M(x,y,z),则有 =%Vx2+y2= 故旋转曲面方程为 f(±Vx2+y2,)=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

建立yoz面上曲线C 绕 z 轴旋转所成曲面的方程: 故旋转曲面方程为 M (x, y,z) , 当绕 z 轴旋转时, f (y1 ,z1 ) = 0 (0, , ) , 若点 M1 y1 z1 C 给定 yoz 面上曲线 C: (0, , ) 1 1 1 M y z M (x, y,z) 1 2 2 1 z = z , x + y = y 则有 ( , ) 0 2 2 f  x + y z = 则有 该点转到 f (y,z) = 0 o z y x C 机动 目录 上页 下页 返回 结束

思考：当曲线C绕y轴旋转时，方程如何？ C:f(y,z)=0 f(y,±Vx2+z2)=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

思考：当曲线 C 绕 y 轴旋转时，方程如何？ C : f (y,z) = 0 o y x z ( , ) 0 2 2 f y  x + z = 机动 目录 上页 下页 返回 结束

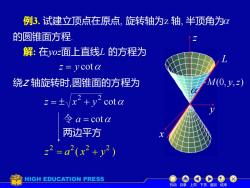
例3.试建立顶点在原点，旋转轴为z轴，半顶角为 的圆锥面方程 解：在0z面上直线L的方程为 z=ycota 绕Z轴旋转时，圆锥面的方程为 M(0,y,2) z=±/x2+y2cota 令a=cota 两边平方 z2=a2(x2+y2) HIGH EDUCATION PRESS 机动目录上页下页返回结束

例3. 试建立顶点在原点, 旋转轴为z 轴, 半顶角为 的圆锥面方程. 解: 在yoz面上直线L 的方程为 绕z 轴旋转时,圆锥面的方程为 ( ) 2 2 2 2 z = a x + y x y z  两边平方 L M (0, y,z) 机动 目录 上页 下页 返回 结束

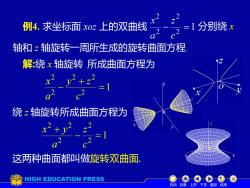
例4.求坐标面xoz上的双曲线 c2=1分别绕x 2 a 轴和z轴旋转一周所生成的旋转曲面方程 解：绕x轴旋转所成曲面方程为 x2y2+2 绕：轴旋转所成曲面方程为 x2+y23 这两种曲面都叫做旋转双曲面. HIGH EDUCATION PRESS 机动目录上页下页返回结束

x y 例4. 求坐标面 xoz 上的双曲线 分别绕 x 轴和 z 轴旋转一周所生成的旋转曲面方程. 解:绕 x 轴旋转 1 2 2 2 2 2 = + − c y z a x 绕 z 轴旋转 1 2 2 2 2 2 − = + c z a x y 这两种曲面都叫做旋转双曲面. 所成曲面方程为 所成曲面方程为 z 机动 目录 上页 下页 返回 结束