《高等数学》课程教学资源（课件讲稿）第八章 向量代数与空间解析几何 8-1 向量及其线性运算

第、章 向量代数与空间解析儿何 平面直角坐标系： s-f,xdx 点一三元数组 空间直角坐标系： 线、面一方程

第八章 平面直角坐标系： 向量代数与空间解析几何 空间直角坐标系： 点 三元数组 线、面 方程

第一节 第八章 句量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影

四、利用坐标作向量的线性运算 第一节 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 五、向量的模、方向角、投影 向量及其线性运算 第八章

一、向量的概念 向量：既有大小，又有方向的量称为向量（又称矢量） 表示法：有向线段MM,或ā 向量的模：向量的大小，记作MM2,或a: 自由向量：与起点无关的向量 M2/ 单位向量：模为1的向量，记作e或e. M 零向量：模为0的向量，记作0，或0

表示法: 向量的模 : 向量的大小, 一、向量的概念 向量: (又称矢量). M1 M 2 既有大小, 又有方向的量称为向量 自由向量:与起点无关的向量. 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量, 有向线段 M1 M2 , 或 a . 记作 e或e

若向量a与b大小相等，方向相同，则称a与b相等 记作a=b, 若量与S方的相时成湘反.层名与4行足作 a/b；规定：零向量与任何向量平行， 与ā的模相同，但方向相反的向量称为ā的负向量 记作一a: 因平行向量可平移到同一直线上，故两向量平行又称 两向量共线 若k(仑3)个向量经平移可移到同一平面上，则称此飞 个向量共面

规定: 零向量与任何向量平行 ; 若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等, 记作 a＝b ; 若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行, a∥b ; 与 a 的模相同, 但方向相反的向量称为 a 的负向量, 记作 因平行向量可平移到同一直线上, 故两向量平行又称 两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 . 记作－a ; a b

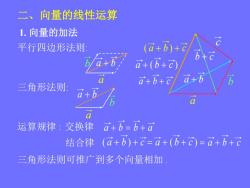
二、向量的线性运算 1.向量的加法 平行四边形法则： (a+b)+c a+(b+c) a+b+c a+b 三角形法则： a a 运算规律：交换律 a+b-b+a 结合律 (a+b)+c-a+(b+c)-a+b+c 三角形法则可推广到多个向量相加

二、向量的线性运算 1. 向量的加法 三角形法则: 平行四边形法则: 运算规律 : 交换律 结合律 三角形法则可推广到多个向量相加 . b b a  b  b  a ( a  b )  c  a  ( b  c )  a  b  c a b c a  b b  c a  ( b  c ) ( a  b )  c a a a  b a  b a  b  c

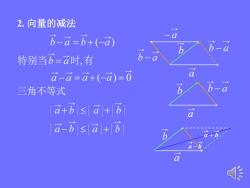
2.向量的减法 b-a=b+(-a) 特别当b=a时，有 - a-a=a+(-a=0 a 三角不等式 a+b≤a+b a-b s a+b 自

2. 向量的减法 三角不等式 a a a

3.向量与数的乘法 2是一个数，入与a的乘积是一个新向量，记作九a 规定：2>0时，2a与a同向，2a=2a 2<0时，2a与a反向，2a=-2a; 2=0时，2a=0. 总之 2a=21a 运算律：结合律2(ua)=u(2a=元ua 分配律(2+四)a=a+ua (a+b)=2a+2万 若a0则有单位向量元，=可d因此d=d同

可见 1a  a  1a  a ; 3. 向量与数的乘法  是一个数 , 规定 : 总之: 运算律 : 结合律 分配律 因此  与 a 的乘积是一个新向量, 记作  a .  a   a ( a )   ( a)    a ( a  b )   a   b 则有单位向量 ea  . 1 a a a a  a e

定理1.设a为非零向量，则 allb 三b=2a (入为唯一实数) 证：“一设石/万，取=士2，a,万同向时取正号 a 反向时取负号，则b与入ā同向，且 故b=a 再证数2的唯一性.设又有b=4a,则(2-)a=0 而a≠0，故2-4=0，即2=4

定理1. 设 a 为非零向量 , 则 ( 为唯一实数) 证: “ ”. , 取 ＝± 且 再证数  的唯一性 . 则 故     0 , 即   . a∥b 设 a∥b 反向时取负号, , a , b 同向时取正号 则 b 与  a 同向, 设又有 b＝ a , (  ) a  0   b 故 b   a

“一”已知b=入a,则 当2=0时，=0 当2>0时，a,b同向 当2<0时，a,b反向 例1.设M为□ABCD对角线的交点，AB=a,AD=b, 试用a与b表示MA,MB,MC,MD 解：a+b=AC=2MC=-2MA b-a=BD=2MD=-2MB . MA=-(a+b)MB=-(6-a) MC=j(a+b) MD=j(b-a)

“ ” 则 例1. 设 M 为 M A B 解: D C ABCD 对角线的交点, b a AC  2 M A BD  2 M B 已知 b＝ a , b＝0 a , b 同向 a , b 反向 a∥b 试 用 a 与 b 表 示 M A, M B , M C , M D . a  b  b  a  ( ) 2 1  M A   a  b ( ) 2 1 M B   b  a ( ) 2 1 M C  a  b ( ) 2 1 M D  b  a

三、空间直角坐标系 笛卡儿的小故事 勒南·第卡尔 有一次，法国著名数学家笛卡儿病了躺在床上， 望着天花板，他看见一只蜘蛛正忙着在墙角上结网， 笛卡儿被吸引住了。他想，这只悬在半空中的蜘蛛， 能不能用两面墙的交线以及墙和地面的交线，来确定 它的位置空间呢？他在纸上画了三条互相垂直的直线 。分别表示两墙的交线和墙与地面的交线。这就建立 了空间直角坐标系

三、空间直角坐标系 勒内·笛卡尔 有一次，法国著名数学家笛卡儿病了躺在床上， 望着天花板，他看见一只蜘蛛正忙着在墙角上结网， 笛卡儿被吸引住了。他想，这只悬在半空中的蜘蛛， 能不能用两面墙的交线以及墙和地面的交线，来确定 它的位置空间呢？他在纸上画了三条互相垂直的直线 。分别表示两墙的交线和墙与地面的交线。这就建立 了空间直角坐标系。 笛卡儿的小故事