《高等数学》课程教学资源（课件讲稿）第十章 多重积分 10-4 重积分应用

第四有 第十章 重积分的应用 一、立体体积 二、曲面的面积 三、物体的质心（自学 四、物体的转动惯量（自学） 五、物体的引力（自学）

第四节 一、立体体积 二、曲面的面积 三、物体的质心(自学) 四、物体的转动惯量(自学) 五、物体的引力(自学) 重积分的应用 第十章

1.能用重积分解决的实际问题的特点： 所求量是 [分布在有界闭域上的整体量 对区域具有可加性 2.用重积分解决问题的方法： 一用微元分析法（元素法）建立积分式 3.解题要点： 画出积分域、选择坐标系、确定积分序、 定出积分限、计算要简便

1. 能用重积分解决的实际问题的特点: 所求量是 对区域具有可加性 —— 用微元分析法 (元素法)建立积分式 分布在有界闭域上的整体量 3. 解题要点: 画出积分域、选择坐标系、确定积分序、 定出积分限、计算要简便 2. 用重积分解决问题的方法:

一、立体体积 ·曲顶柱体的顶为连续曲面z=∫(x,y),(x,y)∈D, 则其体积为 '=∬f(x,y)dxd ·占有空间有界域Ω的立体的体积为 =j∬dxdyd:

一、立体体积 • 曲顶柱体的顶为连续曲面 则其体积为 ( , )d d D V f x y x y   • 占有空间有界域  的立体的体积为 V x y z d d d   

例1.设a>0,计算旋转抛物面x2+y2=az、圆柱面 x2+y2=2ax与平面z=0所围成的立体2的体积 解：方法一：2看作以D={(x,y)1(x-a2+y2≤g2} 为底以：=士+少为顶的曲顶柱体 dG=pdpde =J2d 2acos0 o -dp 4a cos"0d0ma

例1. O z y x 解: 方法一：

例1.设a>0,计算旋转抛物面x2+y2=az、圆柱面 x2+y2=2ax与平面z=0所围成的立体2的体积 解：方法二：在柱面坐标系下Q: 2={p,0,z0≤2≤ 2 0≤p≤2acos0,- ≤0≤ 2 2 r=∬jaw=J∬pod6 =j且dopd 3 24acos0d0=πa3

例1. O z y x 解: 方法二：

二、曲面的面积 设光滑曲面S:z=f(x,y),(x,y)∈D 则面积A可看成曲面上各点M(x,y,z) 处小切平面的面积dA无限积累而成， 它在D上的投影为dσ，则 do=cosy.d4 /1+fx2(x,)+f,2(x,y) dA=/1+f"(x.y)+fy2(x,y)do (称为面积元素)

n  M d A d k 二、曲面的面积 设光滑曲面 则面积 A 可看成曲面上各点 M (x, y,z) 处小切平面的面积 d A 无限积累而成. 它在 D 上的投影为 d , d  cos d A 1 ( , ) ( , ) 1 cos 2 2 f x y f x y  x  y   d 1 ( , ) ( , ) d 2 2 A f x y f x y   x  y (称为面积元素) 则  d ( , ) x y M dA s x y z o  D n 

故有曲面面积公式 4=∬V1+xw+/,ydo 即 dxdy 若光滑曲面方程为x=g(y,),(y,2)EDy:,则有 41+8r÷Fdya:

故有曲面面积公式 2 2 1 ( , ) ( , ) d x y D A f x y f x y      2 2 1 ( ) ( ) d d D z z A x y x y         若光滑曲面方程为 ( , ) , ( , ) , Dy z x  g y z y z  则有 Dy z 即

若光滑曲面方程为y=h(z,x),(2,x)∈Dx,则有 若光滑曲面方程为隐式F(x,y,z)=0,且F≠0，则 0z x F’ ∂y F (x,y)∈Dxy dxdy

2 2 1 ( ) ( ) d d y y A z x z x         若光滑曲面方程为 ( , ) , ( , ) , Dz x y  h z x z x  若光滑曲面方程为隐式 则 则有 x y z y z x x y D F F y z F F x z          , , ( , )   A  Dx y Dz x z x y z F F F F 2 2 2   且 dxd y

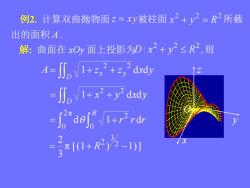
例2.计算双曲抛物面z=xy被柱面x2+y2=R2所截 出的面积A 解：曲面在xOy面上投影为D:x2+y2≤R2,则 A=川nW1+z,2+yddy =∬ny1+x2+y2drd =d061+r2rd I(0+R2)2-1]

例2. 计算双曲抛物面 被柱面 所截 解: 曲面在 xOy 面上投影为 : , 2 2 2 D x  y  R 则 A z z x y D x y 1 d d 2 2     x y x y D 1 d d 2 2     r r r R d 1 d 0 2 2π 0     π [(1 ) 1)] 3 2 2 3 2   R  出的面积 A . z x y O

例3.求球面=√a2-x2-y 被平面 z=h(0<h<a)所截的球冠的面积 解：=Va-x2-y2=h →球冠在xOy面上的投影： D={(m,18g≤a2-0≤0≤2π} X Ja-x-yJa-x-y A=、+*do=a-yo Na-h ap

例3. 求球面 被平面 解: 2 2 2 z a x y    z h h a    (0 ) 所截的球冠的面积. h 2 2 2 z a x y     球冠在xOy面上的投影： z h  D  D O y z x 2 2 2 , x x z a x y     2 2 2 y y z a x y     2 2 1 d x y D A z z      2 2 2 d D a a x y      2 2 {( , ) | 0 - ,0 2 }          a h 2 2 2 2 {( , ) | - } x y x y a h   2 0 d     2 2 - 0 2 2 d a h a a        2 ( ).  a a h