《高等数学》课程教学资源（课件讲稿）第九章多元函数微分法及其应用 9-6 多元函数微分学的几何应用

第之节 第九章 多元菡数微分学的儿何应用 一、一元向量值函数及其导数 二、空间曲线的切线与法平面 三、曲面的切平面与法线

二、空间曲线的切线与法平面 第六节 一、一元向量值函数及其导数 三、曲面的切平面与法线 多元函数微分学的几何应用 第九章

一、一元向量值函数及其导数 引例：已知空间曲线厂的参数方程 x=0(t) y= w(t) te[a,β] z=0(t) 记7=(x,y,z),f()=(o(t),wt),o(t0) T的向量方程F=f(t),t∈[a,B] 此方程确定映射f:a,]→>R,称此映射为一元向量 值函数 对T上的动点M,显然7=OM,即T是子的终点M 的轨迹，此轨迹称为向量值函数的终端曲线 要用向量值品数研究曲孩的莲猿性和光情性，就需要引进向 量值品数的极限、连猿和导数的概念

一、一元向量值函数及其导数 引例: 已知空间曲线  的参数方程: [ , ] ( ) ( ) ( )              t z t y t x t 记 r  (x, y,z), f (t)  ((t),(t),(t))  的向量方程 r  f (t), t [,] M r  x z O y 对 上的动点M , 即 是 此方程确定映射 3 f :[,] R ,称此映射为一元向量 显然r  OM， r 的终点M 的轨迹 , 此轨迹称为向量值函数的终端曲线 . 值函数. 要用向量值函数研究曲线的连续性和光滑性，就需要引进向 量值函数的极限、连续和导数的概念

定义1：给定数集DcR,称映射f:D→R"为一元向量 值函数（简称向量值函数），记为 定义域 T=f(t),tED 因变量 自变量 向量值函数的极限、连续和导数都与各分量的极限 连续和导数密切相关，因此下面仅以=3的情形为代表 进行讨论， 在R中，若向量值函数f(t),t∈D的三个分量函数 依次为f(t),f(t),f(t),1∈D,则向量值函数f(t)可表示为 F(t)=f(t)i+f,(t)j+(t)k,tED 或 f(t)=(f(),f(),f(t),1∈D

定义1: 给定数集 D  R , 称映射 n f : D  R 为一元向量 值函数（简称向量值函数）, 记为 r  f (t), t  D 定义域 因变量 自变量 向量值函数的极限、连续和导数都与各分量的极限、 连续和导数密切相关, 进行讨论. 因此下面仅以 n = 3 的情形为代表 3 ( ), 在R f t t D 中，若向量值函数  的三个分量函数 1 2 3 依次为f t f t f t t D f t ( ), ( ), ( ), , ( )  则向量值函数 可表示为 1 2 3 f t f t i f t j f t k t D ( )= ( ) ( ) ( ) ,    或 1 2 3 f t f t f t f t t D ( )=( ( ), ( ), ( )), 

如空间曲线T的参数方程 x=t M(x,y,z y=t2t∈[0,2] z=t r=OM r=f)=ti+2j+k=(亿，)，t∈[0,2] r=f(0:t∈[0,2]>(t,2,t)

x z O y 如空间曲线  的参数方程: 2 3 [0,2] x t y t t z t          r f t  ( ) M x y z ( , , )  r r f t  ( ) : t [0,2] 2 3  ( , , ) t t t 2 3    ti t j t k 2 3   ( , , ), [0,2] t t t t r OM 

定义2：设向量值函数f()在t的某一去心邻域内有 有定义，如果存在一个常向量，对于V>0,总3δ>0， 使得当满足0 连续：limf(t)=f(o) 10

定义2: 0 设向量值函数 f t t ( ) 在 的某一去心邻域内有 有定义， 0 如果存在一个常向量r，对于   0, 总   0, 0 使得当t t t f t 满足0 , ( )    时 对应的函数值 都满足： 0 f t r ( ) ,    0 0 那么，常向量r f t t t 就叫做向量值函数 ( )当  时的极限， 记作 0 0 lim ( ) t t f t r   0 0 或 f t r t t ( ) , ( )   1 2 3 设 f t f t f t f t t D ( ) ( ( ), ( ), ( )), ,   则 极限： 连续： lim ( ) (lim ( ), lim ( ), lim ( )) 1 2 3 0 0 0 0 f t f t f t f t tt tt tt tt  lim ( ) ( ) 0 0 f t f t t t  

定义3：设向量值函数r=f()在1的某一邻域内有定义， 如果 △r lim lim f(。+△)-f() △1→0△t △1-→0 △t 存在，那么就称这个极限向量为向量值函数f(t)在1处 的导数或导向量，记作 f)或 dr 设f()=(f(t),f(,f(),t∈D,则 导数：f(0=(f),(),f()

定义3: 0 设向量值函数r f t t  ( ) 在 的某一邻域内有定义， 如果 0 lim t r t     0 存在，那么就称这个极限向量为向量值函数 f t t ( )在 处 1 2 3 设 f t f t f t f t t D ( ) ( ( ), ( ), ( )), ,   则 0 0 0 ( ) ( ) lim t f t t f t t        的导数或导向量，记作 0 0 d ( ) . d t t r f t t   或 导数： ( ) ( ( ), ( ), ( )) 1 2 3 f  t  f  t f  t f  t

向量值函数的导数运算法则：P94) 设，下是可导向量值函数，C是常向量，c是任一常数 p(t)是可导函数，则 dC-o (2)Ici()=c'() (3)[i)±】=()±() (4)o)i=p'u)0+p)i) (⑤)0]=00+00 (6) 是I()x】=()x)+)x (7 dpt】=p'(u)[pt)]

向量值函数的导数运算法则: (P94) 设 u, v 是可导向量值函数, (t) 是可导函数, 则 C O t  d d (1) (2) [ ( )] ( ) d d cu t c u t t   (3) [ ( ) ( )] ( ) ( ) d d u t v t u t v t t      (4) [ ( ) ( )] ( ) ( ) ( ) ( ) d d t u t t u t t u t t     (5) [ ( ) ( )] ( ) ( ) ( ) ( ) d d u t v t u t v t u t v t t        (6) [ ( ) ( )] ( ) ( ) ( ) ( ) d d u t v t u t v t u t v t t        C 是常向量, c 是任一常数, (7)  ( ) ( )  ( ) d d u t t u t t    

向量值函数导数的几何意义： 在R3中，设7=f(①)，t∈D的终端曲线为T, OM=f),O=f。+△) f(t) △7=f。+△0-f,) △7 mA=f) 1%△1 设f(,)≠0，则 f'(t)表示终端曲线在t处的一个切向量， 其指向与t的增长方向一致

向量值函数导数的几何意义: 在 R3中, 设 r  f (t), t  D 的终端曲线为 , M  x z O y Δr ( )0 f  t t r Δ Δ ( ), ( Δ ) 0 0 OM  f t ON  f t  t N Δ ( Δ ) ( ) 0 0 r  f t  t  f t ( ) Δ Δ lim 0 0 f t t r t t    表示终端曲线在t0处的一个切向量, 其指向与t 的增长方向一致. ( )0 f  t 设 f (t0 )  0 , 则 r

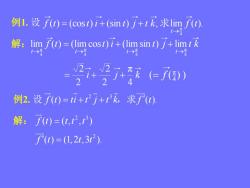
例1.设f0=(cos)i+(sin)j+t元，求1imft） 解：limf()=(lim cost)i+(lim sint)j+limt →1 - 例2.设f)=i+t2j+t元求f(0 解：f()=(,2,) f'(t)=(1,21,32)

( ) (cos ) (sin ) , lim ( ). 4 π f t t i t j t k f t t 例1. 设    求 解： f t t i t j t k t t t t 4 π 4 π 4 π 4 π lim ( ) (lim cos ) (limsin ) lim        i j k 4 π 2 2 2 2    ( ( ) ) 4 π  f 解： 例2. 设 2 3 f t ti t j t k f t ( ) ( ).    ，求  2 3 f t t t t ( ) ( , , )  2 f t t t ( ) (1,2 ,3 ). 

例3.设空间曲线厂的向量方程为 7=f0=(t+1,4t-3,2r2-61),teR 求曲线厂上对应于t。=2的点处的单位切向量 解： f'(t)=(21,4,41-6),1∈R f'(2)=(4,4,-2》 f(2)=V42+4+(-2y2=6 f'(2) 221 故所求单位切向量为 f(2) 3’3’3 其方向与t的增长方向一致 另一与1的增长方向相反的单位切向量为（一 22 3-3

例3. 设空间曲线 的向量方程为 求曲线 上对应于 解: ( ) ( 1, 4 3, 2 6 ) 2 2 r  f t  t  t  t  t 的点处的单位切向量. 故所求单位切向量为 其方向与 t 的增长方向一致 另一与 t 的增长方向相反的单位切向量为 ) 3 1 , 3 2 , 3 2 (   = 6