《高等数学》课程教学资源（课件讲稿）第九章多元函数微分法及其应用 9-4 多元函数求导法则

第四方 第九章 多元复合品数的求导法则 元复合函数 y=f(u),u=p(x) 求导法则 dy dy du dx du dx 微分法则 dy=f"'(u)du=f'(u)o'(x)dx 本节内容： 一、多元复合函数求导的问题 二、多元复合函数的全微分

第四节 一元复合函数 求导法则 本节内容: 一、多元复合函数求导的问题 二、多元复合函数的全微分 微分法则 多元复合函数的求导法则 第九章 yu x

一、多元复合函数求导的问题 1、一元函数与多元函数复合的情形 定理1.若函数u=p(t),v=w(t)在点1可导，z=f(u,v) 在点(u,)处偏导连续，则复合函数z=f(p(t),y(t) 在点t可导，且有链式法则 dz Oz du oz dv dt Ou dt Oy dt 证：设t取增量△t,则相应中间变量 有增量△u,△v, △z= + Ou △y+o(p）(p=△w2+(A2) v

1、一元函数与多元函数复合的情形 定理1. 若函数 z  f (u,v) 处偏导连续, 在点 t 可导, t v v z t u u z t z d d d d d d         z 则复合函数 证: 设 t 取增量△t , v v z u u z z           o (  ) 则相应中间变量 且有链式法则 u v t t 有增量△u ,△v , 一、多元复合函数求导的问题

aEAu+A"+o(P）(p=V(△w2+(Ay2） △t ou△t Ov△t △ 令△t→0，则有△1→0，△v→0， △u du △vdv △t dt' △t dt 0(p) o(p) △t 0 (△1≤0时，根式前加“-号) dz Oz du Oz dv (全导数公式) dt Ou dt Oy dt

则有u  0, v  0, ( 全导数公式 ) t v v z t u u z t z             t o   (  ) z u v t t ( ( ) ( ) ) 2 2   u  v ( )  o   (△t＜0 时,根式前加“–”号) t v t v t u t u d d , d d       t v v z t u u z t z d d d d d d        

记忆：z=f(u,),u=p(t),v=Ψ(t), d=oz du oz dv dt au dt Ov dt 口诀：分段用乘，分叉用加， 单路全导，叉路偏导 推广：讨论中间变量多于两个的情形 设下面所涉及的函数都可微 例如，z=f(u,y,w), u=p(t),v=v(t),w=@(t) dz Oz du Oz dy Oz dw dt Ou dt Oy dt ow dt

推广: 讨论中间变量多于两个的情形. z  f (u,v,w) , 设下面所涉及的函数都可微 .  t z d d z u v w t u u z d d    t v v z d d     t w w z d d     u  (t), v  (t), w  (t) 例如, t t t 记忆: z f u v  ( , ) , u t v t     ( ), ( ), z u v t t  t z d d t u u z d d    t v v z d d     口诀 : 分段用乘, 分叉用加, 单路全导, 叉路偏导

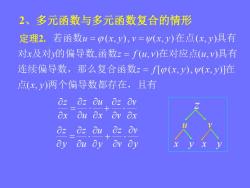
2、多元函数与多元函数复合的情形 定理2.若函数u=p(x,y),V=W(x,y)在点(x,y)具有 对x及对的偏导数，函数z=f(u,v)在对应点(u,v)具有 连续偏导数，那么复合函数z=fp(x,y),W(x,y)]在 点(x,y)两个偏导数都存在，且有 OzOz Ou 0z Ov Ox Ou Ox Bv 8x Oz oz ou Oz Ov ay Ou ay'av ay

2、多元函数与多元函数复合的情形 定理2.    x z    y z z u v x y x u u z      x v v z       y u u z      y v v z       x y

推广：中间变量多于两个的情形 例如，2=f(u,V,w), u=p(x,y),v=w(x,y),w=@(x,y) azaz∂ua2ay,azdw 8x Ou Ox Ov Ox Ow 8x Oz Oz Ou Oz Ov 0z Ow Oy Ou ay Ov ay'Ow ay

中间变量多于两个的情形. z  f (u,v,w) , z u v w u x y v x y w x y       ( , ), ( , ), ( , ) 例如,    x z x u u z      x v v z       z w w x       x yx yx y    y z y u u z      y v v z       z w w y       推广:

3、其他情形 定理3.若函数1=p(x,y)在点(x,y)具有对x及对的 偏导数，函数v=W(y)在点y可导，函数z=f(,v)在 对应点(u,v)具有连续偏导数，那么复合函数z= f[p(x,y),W(y)]在点(x,y)两个偏导数都存在，且有 0z Oz Ou Ox Ou Ox Oz Oz Ou l Oz dv 8y Ou 8y Ov dy

3、其他情形 定理3.    x z    y z z u v x y x u u z      y u u z      d d z v v y     y

又如，z=f(u,x,y),u=p(x,y) 当它们都具有可微条件时，有 0z of ou +贫 8x Ou 8x 0z of ou of =fp+f 0y Ou Oy 0y 注意： 这里 与0 不同 Ox x 表示f(p(x,y),x,y)固定y对x求偏导 f 8x 表示f(u,x,y)固定u和y对x求偏导

又如, z f u x y u x y   ( , , ), ( , )  当它们都具有可微条件时, 有 x z   1 1 2   f f     y z   1 2 3   f f     z  f x y 注意: 这里 x z   x f   x z   x f   f u u x      与 不同, u x y 表示f x y x y y x ( ( , ), , )  固定 对 求偏导 表示f u x y u y x ( , , )固定 和 对 求偏导

又如，z=f(u,x,y),u=p(x,y) 当它们都具有可微条件时，有 0z of ou '9+月 8x Ou 0x 0z of ou Ou =%+乃口诀： 注意： 这里 三与9 不同， 分段用乘，分叉用加 y 单路全导，叉路偏导 0z 表示f((x,y),x,y)固定x对y求偏导 表示f(u,x,y)固定和x对y求偏导 8

又如, z f u x y u x y   ( , , ), ( , )  当它们都具有可微条件时, 有 x z   1 1 2   f f     y z   1 2 3   f f     z  f x y 注意: 这里 z y   f y   z y   f y   口诀 : f u u x      与 不同, 分段用乘, 分叉用加, 单路全导, 叉路偏导 u x y 表示f x y x y x y ( ( , ), , )  固定 对 求偏导 表示f u x y u x y ( , , )固定 和 对 求偏导

例1.设：=e”sin,u=x灯，v=x+y.求，2 Ox oy OzOz Ou Oz Ov 解：xOu0x0x =e"sinv,y+e“cosv.l =ex[y.sin(x+y)+cos(x+y)] OzOz Ou 0z 0v 10 0y Ou ay'Ov 8y =e"sinv.x+e"cosv.1 e[x.sin(x+y)+cos(x+y)]

例1. 设 z e sin v, u xy , v x y , u     , . y z x z     求 解: x z   v u  e sin y z   v u  e sin x v v z       v u  e cos y v v z       v u  e cos 1 1 z u v x y x y