《高等数学》课程教学资源（PPT课件，上册）函数的微分

§2.5函数的微分 微分的概念 二、微分的几何意义 三、微分的运算法测 四、微分在近似计算中的应用

山东农业大学 高等数学 主讲人：苏本堂 二、微分的几何意义 一、微分的概念 §2.5函数的微分 三、微分的运算法则 四、微分在近似计算中的应用

一、微分的概念 引例：一块正方形金属薄片受温度变化的影响，其 边长由xo变到x,+△x,问此薄片面积改变了多少？ 设薄片边长为x,面积为A,则A=x2,当x在x取 得增量△x时，面积的增量为 A4=(+△x)2-x2 △x x0△x (4)2 2x0Ar +(Ar) 关于△x的△x→0时为 Xo A=x 线性主部高阶无穷小 故 △A≈2xAx 称为函数在xo的微分

山东农业大学 高等数学 主讲人：苏本堂 一、微分的概念 引例: 一块正方形金属薄片受温度变化的影响, 问此薄片面积改变了多少? 设薄片边长为x , 面积为 A , 则 , 2 A = x 0 x x 面积的增量为 x x 0 2 0 A = x x x 0 2 (x) 关于△x 的 线性主部 高阶无穷小 x →0 时为 故 称为函数在 x0 的微分 当 x 在 0 x 取 得增量 x 时, 0 x 变到 , 0 边长由 x + x 其

定义：若函数y=∫(x)在点xo的增量可表示为 △y=f(xo+△)-f(xo)=A△x+o(△x) (A为不依赖于△x的常数) 则称函数y=f(x)在点x可微，而A△x称为f(x)在 点xo的微分，记作dy或df,即 dy=A△x 定理：函数y=∫(x)在点xo可微的充要条件是 y=f(x)在点xo处可导，且A=∫'(xo),即 dy=f'(xo)△x

山东农业大学 高等数学 主讲人：苏本堂 的微分, 定义: 若函数 在点 x0 的增量可表示为 ( A 为不依赖于△x 的常数) 则称函数 y = f (x) 而 Ax 称为 记作 即 dy = Ax 定理: 函数 在点 x0 可微的充要条件是 = Ax + o(x) 即 dy = f (x )x 0 在点 可微

定理：函数y=f(x)在点x,可微的充要条件是 y=f(x)在点o处可导，且A=∫'(xo),即 dy=f'(xo)△x 证：“必要性” 已知y=f(x)在点xo可微，则 △y=f(xo+△x)-f(xo)=A△x+o(△x) 是4+=4 △x-→0△X△x-→0 故y=(x)在点xo的可导，且∫'(xo)=A

山东农业大学 高等数学 主讲人：苏本堂 定理 : 函数 证: “必要性” 已知 在点 可微 , 则 ( ) ( ) 0 0  y = f x + x − f x ) ( ) lim lim ( 0 0 x o x A x y x x   = +     →  → = A 故 = Ax + o(x) 在点 的可导, 且 在点 x0 可微的充要条件是 在点 处可导, 且 即 dy = f (x )x 0

山东农业大发 等数雪 主讲人：苏本堂 定理：函数y=∫(x)在点x可微的充要条件是 y=f(x)在点x处可导，且A=f'(xo),即 dy=f'(xo)△x “充分性”已知y=f(x)在点x的可导，则 lim △y=f'(xo) △x→0△x A=f)+a（mx=0） △ 故△y=f'(x)△x+△x=f'(xo)Ax+o(△x) 线性主部 (f'(xo)≠0时) 即dy=f'(xo)△x

山东农业大学 高等数学 主讲人：苏本堂 定理 : 函数 在点 x0 可微的充要条件是 在点 处可导, 且 即 dy = f (x )x 0 “充分性”已知 lim ( ) 0 0 f x x y x =     → =  +    ( ) 0 f x x y ( lim 0 ) 0 =  →  x y = f (x )x +x 故 0 ( ) ( ) 0 = f  x x + o x  线性主部 即 dy = f (x )x 0 在点 的可导, 则

注：△y=f'(xo)△x+o(△x) dy=f'(xo)△x 当f'(xo)≠0时， lim △y=1im △y Ax->0dy △x-0f'(x0)△x △y lim =1 f(xo)Ax->0 Ax 所以△x→0时△y与dy是等价无穷小，故当△x 很小时，有近似公式 △y≈dy

山东农业大学 高等数学 主讲人：苏本堂 注: f (x0 )  0 时 , dy = f (x )x 0 ( ) ( ) 0 y = f  x x + o x y y x d lim 0   → f x x y x    =  → ( ) lim 0 0 x y f x x    =  →0 0 lim ( ) 1 =1 所以 x → 0 时 y dy 很小时, 有近似公式 x y  dy 与 是等价无穷小, 当 故当

=x)在点x可微台△=A△x+o(△x).d=f'(xo)△x· 例1求函数y=x2在x=1和=3处的微分. 解函数y=x2在x=1处的微分为 dy=(x2)Lkx=1△x=2Ax; 函数y=x2在=3处的微分为 d=(x2)儿x=3△x=6Ax. 例2求函数y=x3当x=2,△x=0.02时的微分 解先求函数在任意点x的微分， dy=(x3)'△=3x2Ax. 再求函数当x=2,Dx=0.02时的微分， dy-2,A-0.02=3x21x=2.A0.02=3×22×0.02=0.24

山东农业大学 高等数学 主讲人：苏本堂 例1 求函数y=x 2在x=1和x=3处的微分 dy=(x 2 )|x=1x=2x 函数y=x 2在x=3处的微分为 dy=(x 2 )|x=3x=6x 例2 求函数 y=x 3当x=2 x =002时的微分 y=f(x)在点x0可微y=Ax+o(x) dy= f (x0 )x  解 函数y=x 2在x=1处的微分为 解 先求函数在任意点x的微分 dy=(x 3 )x=3x 2x 再求函数当x=2 Dx=002时的微分 dy| x=2, x=0.02 =32 2 =3x 0.02=0.24 2 | x=2, x=0.02

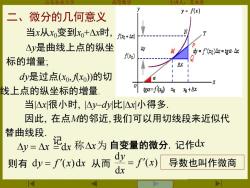
y=f(x) 二、微分的几何意义 当x从x变到x+△x时， +△的 △y是曲线上点的纵坐 y y='"0)4=gx 标的增量； dy是过点(xo,xo)的切 线上点的纵坐标的增量 0 gC=f6)和为+x 当△x很小时，△y-dy比△x小得多. 因此，在点M的邻近，我们可以用切线段来近似代 替曲线段， △y=Ardx称Ax为自变量的微分，记作d 则有dy=了x从而=了导数也叫作微酒

山东农业大学 高等数学 主讲人：苏本堂 当|x|很小时 |y−dy|比|x|小得多 因此 在点M的邻近 我们可以用切线段来近似代 替曲线段 y是曲线上点的纵坐 标的增量; dy是过点(x0  f(x0 ))的切 线上点的纵坐标的增量. 当x从x0变到x0+x时 二、微分的几何意义 则有 dy = f (x)dx 从而 ( ) d d f x x y =  导数也叫作微商 称x为 自变量的微分, 记作 dx y = x = dx 记

三、微分的基本公式和运算法则 1.基本初等函数的微分公式 导数公式： 微分公式： (x4'=ux- d(xi)=ux-dx (sin x)'=cos x d(sinx)=cos xdx (cos x)'=-sinx d(cos x)=-sin xdx (tanx)'=sec2x d(tanx)=sec2xdx (cot x)'=-csc2x d(cotx)=-csc2xdx (sec x)'=secx tanx d(secx)=secx tan xdx (csc x)'=-cscx cotx d(cscx)=-cscx cot xdx (ax)'=a*In a d(ax)=ax In adx (ex)=ex d(ex)=exdx

山东农业大学 高等数学 主讲人：苏本堂 d(x m )=m x m−1dx d(sin x)=cos xdx d(cos x)=−sin xdx d(tan x)=sec2xdx d(cot x)=−csc2xdx d(sec x)=sec x tan xdx d(csc x)=−csc x cot xdx d(a x )=a x ln adx d(e x )=e xdx (x m )=m x m−1 (sin x)=cos x (cos x)=−sin x (tan x)=sec2 x (cot x)=−csc2x (sec x)=sec x tan x (csc x)=−csc x cot x (a x )=a x ln a (e x )=e x 导数公式: 微分公式: 1.基本初等函数的微分公式 三、微分的基本公式和运算法则

导数公式： 微分公式： (lOgax)=- d(logax)=- dx na Ina (n= d(Inx)=1dx x (arcsinx)'= √-x2 d(arcsinx)x (arccosx)'=- 1 d(arccosx)=- 1 dx √1-x2 √1-x2 (arctanx)'= 1+x2 d(arctanx)=1+x (arccotx)'=- 1 1+x2 d(arecot)=-, 1+r2

山东农业大学 高等数学 主讲人：苏本堂 x a x a ln 1 (log ) = x x 1 (ln ) = 1 2 1 (arcsin ) x x −  = 1 2 1 (arccos ) x x −  =− 1 2 1 (arctan ) x x +  = 1 2 1 (arccot ) x x +  =− dx x a d x a ln 1 (log )= dx x d x 1 (ln )= dx x d x 1 2 1 (arcsin ) − = dx x d x 1 2 1 (arccos ) − =− dx x d x 1 2 1 (arctan ) + = dx x d x 1 2 1 (arccot ) + =− 导数公式: 微分公式: