《高等数学》课程教学资源（PPT课件，上册）换元积分法

第二节换元积分法 一、第一类换元法 二、第二类换元法

山东农业大学 高等数学 主讲人：苏本堂 第二节换元积分法 一、第一类换元法 二、第二类换元法

山东农业大 方本 一、第一类换元法 问题 「cos2 xdx sin2x+C, 解决方法 利用复合函数，设置中间变量. 过程 令t=2x→dk=二t, 12 ∫cos2xk=2打o=2sint+C=2sin2x+C, 在一般情况下： 设F'(w=f(w),则f(u)du=F(w)+C. 如果u=p(x)（可微)：'dFIp(x)川=fIp(x)川p'(x) ·.∫f[p(x)lp'(x)d=FLp(xl+C-=lf(w)dl-pe 由此可得换元法定理

山东农业大学 高等数学 主讲人：苏本堂  cos2xdx= sin2x + C, 利用复合函数，设置中间变量. 令 t = 2x , 2 1  dx = dt  cos2xdx tdt  = cos 2 1 = sint + C 2 1 sin2 . 2 1 = x + C 问题 解决方法 过程 一、第一类换元法 设 F(u) = f (u), 则 ( ) ( ) .  f u du = F u + C 如果 u = (x) （可微）  dF[(x)] = f[(x)](x)dx   f[(x)](x)dx = F[(x)]+ C=  = ( ) [ ( ) ] u du u x f  由此可得换元法定理 在一般情况下：

一、第一类换元法 定理1.设f(w)有原函数，u=p(x)可导，则有换元 公式 ∫fIe(lo'cxte=∫fau=oy 即 「fp(x)]o'(x)dx=「f(p(x)dp(x) 第一类换元公式（凑微分法） 注：在一般情况下： 设F'(u)=f(u)则∫f(w)du=F(w)+C 使用此公式的关键在于将 g(x)c化为∫fp(xp'(x)

山东农业大学 高等数学 主讲人：苏本堂 一、第一类换元法 定理1. 设 f (u)有原函数, u =(x)可导, 则有换元 公式  f (u)du u =(x)  即  = f ((x))d(x)  f [(x)] (x)dx 第一类换元公式（凑微分法） 在一般情况下： 设 F'(u) = f (u) 则  f (u)du = F(u)+C 使用此公式的关键在于将  g(x)dx化为  f[(x)]'(x)dx 注:

等数学 主讲 苏本堂 例1求 3+2 解 t21.1.3+2xy, 3+2x23+2x 1324c-32e（3+2如ih -g如=n+(-3+2+c 一般地 ∫fac+b)k=foi.sw

山东农业大学 高等数学 主讲人：苏本堂 例1 求 . 3 2 1 dx x  + 解 (3 2 ) , 3 2 1 2 1 3 2 1  +  + =  + x x x dx x  3 + 2 1 x dx x (3 2 ) 3 2 1 2 1  +  + =  du u  = 1 2 1 = lnu + C 2 1 ln(3 2 ) . 2 1 = + x + C  f (ax + b)dx =  u du u=ax+b f a [ ( ) ] 1 一般地

例2求∫2xe 解：∫2xek=∫edr)"∫e=e+c=e+c 例3求树+2n时 解：∫+2n点-小1n d(1+2Inx) 4=1+2Inx J2加=na+c=21+2n+c

山东农业大学 高等数学 主讲人：苏本堂 例2 求  xe dx x 2 2 解：    = xe dx = e d x = e du u u x x x 2 2 2 2 ( ) 2 e C e C u x = + = + 2 求 解： dx x x  (1+ 2ln ) 1 (ln ) 1 2ln 1 d x x  + = (1 2ln ) 1 2ln 1 2 1 d x x + + =  u = 1+ 2ln x  = du u 1 2 1 = ln u+C 2 1 ln(1 2ln ) . 2 1 = + x +C 例3 dx x x  (1+ 2ln ) 1

等数学 本 dx 想到公式 du arctan u+C 令w ,则du=1dx a a a

山东农业大学 高等数学 主讲人：苏本堂  + = 2 2 1 ( ) 1 d a x x a 例4. 求 解: , a x 令 u = 则 x a u d 1 d =  + 2 1 u du a 1 u C a = arctan + 1 想到公式  + 2 1 d u u = arctan u +C ( ) a x =

a0 dx 小8 arcsin+C a 想到 du arcsinu+C ∫fIo(xp'(x)r=∫f(p(x)dp(x)(直接配元)

山东农业大学 高等数学 主讲人：苏本堂 例5. 求 = −  2 1 d u u 想到 arcsinu +C 解:  − 2 1 ( ) d a x a x  f ((x))d(x) = (直接配元)   f [(x)] (x)dx  − = 2 1 ( ) d ( ) a x a x

山东农业大 高等数学 主讲人：苏本堂 dx 例6.求 2-a2 解： nt0”-ad x2-a2-2a (x-a)(x+a)2 原式=出。小a] da- fn -al-lnx+dll+ +C x+a

山东农业大学 高等数学 主讲人：苏本堂 C x a x a a + + − = ln 2 1 例6. 求 解: 2 2 1 x − a  (x − a)(x + a) (x + a) − (x − a) 2a 1 = ) 1 1 ( 2 1 a x a x + a − − = ∴ 原式 =    2a 1   + − − x a x x a dx d       = 2a 1  − − x a d(x a)     2a 1 = ln x − a − ln x + a +C  + + − x a d(x a)

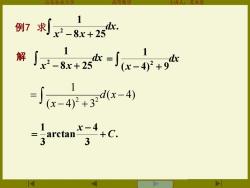
jk-8x+2sc=-x-g 解 -a4- C. 1 3

山东农业大学 高等数学 主讲人：苏本堂 例7 求 . 8 25 1 2 dx x x  − + 解 dx x x  − 8 + 25 1 2 dx x  − + = ( 4) 9 1 2 . 3 4 arctan 3 1 C x + − = ( 4) ( 4) 3 1 2 2 − − + =  d x x

方本 例8.求「tanxdx 解jn冰-品= =-In cos x +C 类似 m水-jm-j In sinx +C

山东农业大学 高等数学 主讲人：苏本堂 例8. 求 解:  x x x d cos sin  = − x x cos dcos  x x x sin cos d  = x x sin dsin 类似