《高等数学》课程教学资源（PPT课件，上册）定积分的概念与性质

高等数学 主计 本堂 第五章定积分 第一节 定积分的概念与性质 第二节 微积分基本公式 第三节 定积分的换元法和分部积分法 第四节 反常积分

山东农业大学 高等数学 主讲人：苏本堂 第五章 定积分 第一节 定积分的概念与性质 第二节 微积分基本公式 第三节 定积分的换元法和分部积分法 第四节 反常积分

第一节 定积分的概念与性质 一、定积分问题举例 二、定积分的定义 三、定积分的性质

山东农业大学 高等数学 主讲人：苏本堂 第一节 定积分的概念与性质 三、定积分的性质 一、定积分问题举例 二、定积分的定义

一、定积分问题举例 在初等函数里面，我们只会计算规则图形的面积， 如长方形，圆形等。如何计算不规则图形的面积，是 我们需要解决的问题。 曲边梯形 设函数y=x)在区间[a,b] =孔x) 上非负、连续.由直线x=a、x=b、 y=O及曲线y=fx)所围成的图形 x-a x=b 称为曲边梯形，其中曲线弧称 为曲边 0 L b 如何计算其面积？

山东农业大学 高等数学 主讲人：苏本堂 一、定积分问题举例 曲边梯形 设函数y=f(x)在区间[a, b] 上非负、连续. 由直线x=a、x=b、 y=0及曲线y=f(x)所围成的图形 称为曲边梯形, 其中曲线弧称 为曲边. 如何计算其面积？ a b x y o y=f(x) x=a x=b 在初等函数里面，我们只会计算规则图形的面积， 如长方形，圆形等。如何计算不规则图形的面积，是 我们需要解决的问题

解决步骤： 1)分割. 在区间[a,b]中任意插入n-1个分点 a=0<1<x2<<xn-1<Xn=b 用直线x=x;将曲边梯形分成n个小曲边梯形， 2)近似.在第i个窄曲边梯形上任取5：∈[x;-1,x;] 1 作以[x-1,x]为底，f(5) 为高的小矩形，并以此小 梯形面积近似代替相应 窄曲边梯形面积△A,得 a x xXi-1xi bx 51 △4≈f(5i)△xi(Axi=x-x-1),i=1,2,.,n)

山东农业大学 高等数学 主讲人：苏本堂 1 x i x i−1 a x y o 解决步骤 : 1) 分割. 在区间 [a , b] 中任意插入 n –1 个分点 a = x0  x1  x2  xn−1  xn = b [ , ] i i 1 i x x   − 用直线 i x = x 将曲边梯形分成 n 个小曲边梯形; 2) 近似. 在第i 个窄曲边梯形上任取 作以 [ , ] i 1 i x x − 为底 , ( )i f  为高的小矩形, 并以此小 梯形面积近似代替相应 窄曲边梯形面积 得 ( ) ( )  i  i  i  i = i − i−1 A f  x x x x  i

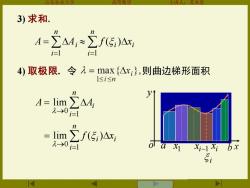
主讲 苏本堂 3)求和. A=∑A4,≈∑f(5:)△x 1 i=l 4)取极限.令元=max{△r;},则曲边梯形面积 l≤i≤n n A=lim∑A4, 1→01 = lim ∑f(5i)Ax: 201 Xi-1xi bx

山东农业大学 高等数学 主讲人：苏本堂 3) 求和.  = =  n i A Ai 1  =   n i i i f x 1 ( ) 4) 取极限. 令 则曲边梯形面积  → = =  n i A Ai 1 0 lim   → = =  n i i i f x 1 0 lim ( )  a y o 1 x i x i−1 x  i

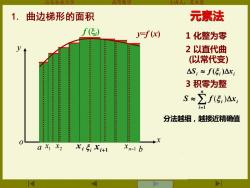
苏本宜 1.曲边梯形的面积 元素法 f() =f(x) 1化整为零 2以直代曲 (以常代变) △S:≈f(5:)△x: 3积零为整 防a S≈ 分法越细，越接近精确值 a x X2 5 Xn-1 b

山东农业大学 高等数学 主讲人：苏本堂 xi xi+1 1 x i x2  元素法 1 化整为零 2 以直代曲 (以常代变) i i xi S  f ( ) 3 积零为整 y x o y=f (x) n−1 x =   n i i xi S f 1 ( ) a b . . 分法越细，越接近精确值 1. 曲边梯形的面积 f (i )

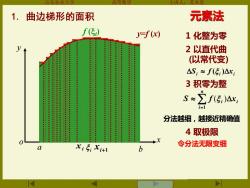
山东农业大 导效 主 苏本堂 1.曲边梯形的面积 元素法 yf(x) 1化整为零 2以直代曲 (以常代变) △S,≈f(5)△c: 3积零为整 S≈ ∑f5)△x, i= 分法越细，越接近精确值 4取极限 5 令分法无限变细 i+1 b

山东农业大学 高等数学 主讲人：苏本堂 xi i xi+1  元素法 4 取极限 y x o y=f (x) 令分法无限变细 . a . b . . 分法越细，越接近精确值 1 化整为零 2 以直代曲 (以常代变) 3 积零为整 =   n i i xi S f 1 ( ) i i xi S  f ( ) f (i ) 1. 曲边梯形的面积

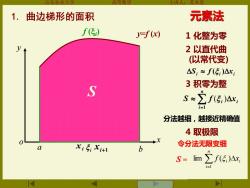
1.曲边梯形的面积 元素法 f(传) =f(x) 1化整为零 2以直代曲 (以常代变) △S:≈f(5:)△x 3积零为整 )ar S≈ 分法越细，越接近精确值 4取极限 Xi+ 令分法无限变细 b S=m∑f(5,)Ax, i=1

山东农业大学 高等数学 主讲人：苏本堂 xi i xi+1  元素法 4 取极限 y x o y=f (x) 令分法无限变细 . . . . 分法越细，越接近精确值 1 化整为零 2 以直代曲 (以常代变) 3 积零为整 =   n i i xi S f 1 ( ) i i xi S  f ( ) f (i ) =  n i i i f x 1 S = lim ( ) . S . a b 1. 曲边梯形的面积

山东农业大 2.变速直线运动的路程 已知物体直线运动的速度y=v()是时间t的连续函数， 且v(t)≥0，计算物体在时间段[T,T,]内所经过的路程S: (I)分割：T=t<t<t2.<tn-1<t,=T2△t=t-t-1 (2)近似：物体在时间段[-1，内所经过的路程近似为 △S,v()△t,（t-1<t;<t)月 (3)和：物体在时间段[T1,T2]内所经过的路程近似为 S≈2c,)AM； (4)取极限：记=max{△t1,△12，△1n},物体所经过的路程为 S=lim∑(t)△t,. -→0 i=l

山东农业大学 高等数学 主讲人：苏本堂 2.变速直线运动的路程 已知物体直线运动的速度v=v(t)是时间 t 的连续函数, 且v(t)0, 计算物体在时间段[T1 , T2 ]内所经过的路程S. (1)分割: T1=t 0<t 1<t 2<  <t n−1<t n =T2 , t i=t i−t i−1 ; (2)近似: 物体在时间段[t i−1 , t i ]内所经过的路程近似为 Siv(i )t i ( t i−1< i<t i ); 物体在时间段[T1 , T2 (3)求和: ]内所经过的路程近似为 (4)取极限: 记=max{t 1 , t 2 ,, t n }, 物体所经过的路程为  =   n i i i S v t 1 ( )   → = =  n i i i S v t 1 0 lim ( )  

1.曲边梯形的面积 2.变速直线运动的路程 S=lim ∑f(5)△x s=lim∑v(5:)△t 1→0 i=l 入→01 上述两个问题的共性： •解决问题的方法步骤相同： “分割，近似，求和，取极限” ·所求量极限结构式相同：特殊乘积和式的极限 许多问题的解决都可以化为上述特定和式的问题， 将其一般化，就得到定积分的概念

山东农业大学 高等数学 主讲人：苏本堂 上述两个问题的共性: • 解决问题的方法步骤相同 : “分割 , 近似 , 求和 , 取极限 ” • 所求量极限结构式相同: 特殊乘积和式的极限 1. 曲边梯形的面积 2.变速直线运动的路程 = → =  n i i i S f x 1 0 lim ( )  许多问题的解决都可以化为上述特定和式的问题， 将其一般化，就得到定积分的概念