《高等数学》课程教学资源（PPT课件，下册）向量及其运算

山东农业大学 第八章 空间解析几何与向量代数 第一节 向量及其线性运算 第二节 数量积向量积*混合积 第三节 平面及其方程 第四节 空间直线及其方程 第五节 曲面及其方程 第六节 空间曲线及其方程

山东农业大学 高等数学 主讲人：苏本堂 第八章 空间解析几何与向量代数 第一节 向量及其线性运算 第二节 数量积 向量积 *混合积 第三节 平面及其方程 第四节 空间直线及其方程 第五节 曲面及其方程 第六节 空间曲线及其方程

率数学 主计 方本 §8.1向量及其运算 一、 向量概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影

山东农业大学 高等数学 主讲人：苏本堂 一、向量概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影 §8.1 向量及其运算

一、向量的概念 向量：既有大小，又有方向的量称为向量（又称矢量） 表示法：有向线段MM,或a,或a. 向量的模：向量的大小，记作M1M2,或a,或a 向径（矢径）：起点为原点的向量， 自由向量：与起点无关的向量 M2 单位向量：模为1的向量，记作°或a°. M 零向量：模为0的向量，记作0，或0

山东农业大学 高等数学 主讲人：苏本堂 表示法: 向量的模 : 向量的大小, 一、向量的概念 向量: (又称矢量). M1 M2 既有大小, 又有方向的量称为向量 向径 (矢径): 自由向量: 与起点无关的向量. 起点为原点的向量. 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量, 有向线段 M1 M2 , 或 a

若向量ā与b大小相等，方向相同，则称a与b相等， 记作a=b; 若向量a与b方向相同或相反，则称ā与b平行，记作 a∥b；规定：零向量与任何向量平行； 与ā的模相同，但方向相反的向量称为a的负向量， 记作-a; 因平行向量可平移到同一直线上，故两向量平行又称 两向量共线 若k(仑3)个向量经平移可移到同一平面上，则称此k 个向量共面

山东农业大学 高等数学 主讲人：苏本堂 规定: 零向量与任何向量平行 ; 若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等, 记作 a＝b ; 若向量 a 与 b 方向相同或相反,则称 a 与 b 平行, a∥b ; 与 a 的模相同, 但方向相反的向量称为 a 的负向量, 记作 因平行向量可平移到同一直线上, 故两向量平行又称 两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 . 记作－a ;

二、向量的线性运算 1.向量的加法 平行四边形法测： (a+B)+c a+(b+c) a 可+方 三角形法则： a a 运算规律：交换律 a+b-b+a 结合律 (a+b)+c-a+(b+c)=a+b+c 三角形法则可推广到多个向量相加

山东农业大学 高等数学 主讲人：苏本堂 二、向量的线性运算 1. 向量的加法 三角形法则: 平行四边形法则: 运算规律 : 交换律 结合律 三角形法则可推广到多个向量相加 . b b a + b = b + a ( a + b ) + c = a + (b + c ) = a + b + c a b c a + b b + c a + (b + c ) ( a + b ) + c a a a + b a + b

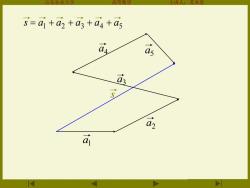
1东农大 等数雪 主讲人：苏本堂 =☑1+a2+a3+a4+a5 g 4 a a

山东农业大学 高等数学 主讲人：苏本堂 s a3 a4 a5 a2 a1 1 2 3 4 5 s = a + a + a + a + a

2.向量的减法 6-d=b+(-a -a -à b-a 特别当b=a时，有 a-a-a+(-a)-0 a 三角不等式 a+b≤a+b a-b≤a+b P DI

山东农业大学 高等数学 主讲人：苏本堂 2. 向量的减法 三角不等式 a

1-/ 3.向量与数的乘法 入是一个数，入与a的乘积是一个新向量，记作2d. 规定：>0时，a与ā同向，a=2d; <0时，a与a反向，a=-a; =0时，a=0. 总之： aa=n a 运算律：结合律(ud)=u(2d)=ud 分配律(+)a=九a+ud 2(a+b)=元a+2b 若#0，则有单位向量a=日a 因此a=aa

山东农业大学 高等数学 主讲人：苏本堂 a a    =  3. 向量与数的乘法  是一个数 , a .   规定 : 1a a ;   = 可见 1a a ;   − = −  与 a 的乘积是一个新向量, 记作 总之: 运算律 : 结合律 ( a)    ( a)  =   a  =   分配律 (a b)    + a b   =  +  =  则有单位向量 a . 1 a a   因此    a = a a

定理1.设a为非零向量，则 allb 三方=人a(八为唯一实数) 直线上点的坐标 点P一向量OP=xi·一实数x 轴上点P的坐标为x的充分必要条件是OP=xi 平面上点的坐标 点M一向量OM=OP+PM =0P+00=xi+yj=(x,y) M 轴上点M的坐标为(x,y)的充分 必要条件是OM=xi+yj

山东农业大学 高等数学 主讲人：苏本堂 定理1. 设 a 为非零向量 , 则 ( 为唯一实数) a∥b ． ． O i P x 点P OP = xi 实数x x 轴上点P的坐标为x的充分必要条件是 OP = xi 直线上点的坐标 平面上点的坐标 O Q p M x y i j 点M 向量 OM OP PM = + = + OP OQ = + x i y j = ( , ) x y 轴上点M的坐标为（x，y）的充分 必要条件是 OM = + x i y j 向量

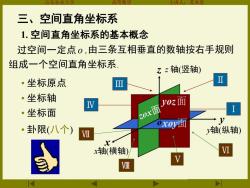
办本堂 三、空间直角坐标系 1.空间直角坐标系的基本概念 过空间一定点0，由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系 zz轴（竖轴） ·坐标原点 m ·坐标轴 y0z面 ·坐标面 0x面 +V 卦限（八个） 0x0面 轴（纵轴） x轴（横轴）

山东农业大学 高等数学 主讲人：苏本堂 Ⅶ Ⅱ Ⅲ Ⅵ x y z Ⅴ Ⅷ Ⅳ 三、空间直角坐标系 由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系. • 坐标原点 • 坐标轴 x轴(横轴) y轴(纵轴) z 轴(竖轴) 过空间一定点o , o • 坐标面 • 卦限(八个) xoy面 yoz面 1. 空间直角坐标系的基本概念 Ⅰ