《高等数学》课程教学资源（PPT课件，下册）第十章 习题课

本 第十章习题课 一、 重积分计算的基本方法 二、重积分计算的基本技巧 三、重积分的应用

山东农业大学 高等数学 主讲人：苏本堂 第十章习题课 一、重积分计算的基本方法 二、重积分计算的基本技巧 三、重积分的应用

山东夜 二、二重积分的定义 1.定义：设f(x,y)是定义在有界区域D上的有界函数， 将区域D任意分成n个小区域△o(i=1,2,.,n), 任取一点(5，)∈△o,若存在一个常数I,使 I=lim 230 ∑f(5,1,)△o 记作 川nfa,)do i=1 则称f(x,y)/何积，称I为f(x,y)在D上的二重积分 积分和 积分表达式 f(x,y)do x,y称为积分变量 积分域 被积函数 面积元素

山东农业大学 高等数学 主讲人：苏本堂 二、二重积分的定义 １.定义: 设 f (x, y) 将区域 D 任意分成n 个小区域 任取一点 若存在一个常数 I , 使 则称 f (x, y) 可积 , 称I为 f (x, y) 在D上的二重积分. x, y称为积分变量 积分和 积分域 被积函数 积分表达式 面积元素 记作 是定义在有界区域 D上的有界函数

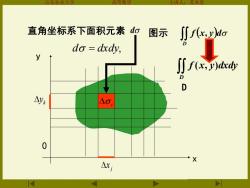
主计 本堂 直角坐标系下面积元素o图示 ∬fx,yo D do dxdy, y ∫∬f(x& D D △yk 0 △x

山东农业大学 高等数学 主讲人：苏本堂 0 x y D j x  i 直角坐标系下面积元素 d 图示  D f (x, y)dxdy d = dxdy, ( )  D f x, y d k y

如果f(x,y)在D上可积，可用平行坐标轴的直线来划 分区域D,这时△o:=△r,Ay,因此面积元素do也常 记作dxdy,二重积分记作 f(x.y)dxdy 引例1中曲顶柱体体积： v=f(xy)do=f(x.y)dxdy 引例2中平面薄板的质量： M=S p(x.y)do -Sp(x.y)dxdy

山东农业大学 高等数学 主讲人：苏本堂  = D V f (x, y)d 引例1中曲顶柱体体积:  = D M  (x, y)d 引例2中平面薄板的质量: 如果 f (x, y) 在D上可积, 也常 dxdy, 二重积分记作 ( , )d d . D f x y x y 分区域D , 这时 因此面积元素 可用平行坐标轴的直线来划 记作  = D f (x, y)d x d y  = D  (x, y)d x d y

2.注解： (1)二重积分的存在性：若函数f(x,y)在有界闭区域 上连续，则f(x,y)在D上可积. (2)二重积分几何意义： 当被积函数大于零时，二重积分是柱体的体积. 当被积函数小于零时，二重积分是柱体的体积的 负值

山东农业大学 高等数学 主讲人：苏本堂 2.注解: (1)二重积分的存在性：若函数 在D上可积. 在有界闭区域 上连续,则 (２)二重积分几何意义： 当被积函数大于零时，二重积分是柱体的体积． 当被积函数小于零时，二重积分是柱体的体积的 负值．

三、二重积分的性质 定积分的性质 性质1当伪常数时， 性质1 dada. fx)=k心fx)d 性质2 性质2 Jf(x,)±g(x,ydo f(x)±g(x) =fx,yao±gx,川do.=fx±gae)

山东农业大学 高等数学 主讲人：苏本堂 三、二重积分的性质 性质１ 当 k 为常数时， ( , ) ( , ) .   = D D kf x y d k f x y d 性质２   D [ f (x, y) g(x, y)]d ( , ) ( , ) .   =  D D f x y d g x y d 定积分的性质   = b a b a k f(x)dx k f (x)dx 性质１   b a [ f (x) g(x)]dx =  b a f (x)dx  b a g(x)dx . 性质２

本 性质3对区域具有可加性 性质3 (D=D+D2) ∬fx,y)o f(x)dx ∬fx,ao+∬fx,yado.=gfx&+f(x) = D D, 性质4 性质4 若o为D的面积， f21dc=∫dc=b-a. o=∬j1-ao-∬o

山东农业大学 高等数学 主讲人：苏本堂 性质３ 对区域具有可加性 ( ) D = D1 + D2  D f (x, y)d ( , ) ( , ) . 1 2   = + D D f x y d f x y d 性质３  b a f (x)dx =  +  b c c a f (x)dx f (x)dx . 若  为D的面积， 1 .   =  = D D  d d 性质4 dx b a   1 dx b a = = b − a. 性质4

性质5若在D上 性质5如果在[a,b上 f(x,y)≤g(x,), f(x)≤g(x) 则有 ∬f.ydo≤∬gxdo. 则旷心fx≤g(xk 特殊地 特殊地 d.Ifxs广fe

山东农业大学 高等数学 主讲人：苏本堂 性质５ 若在D上 f (x, y)  g(x, y), ( , ) ( , ) .    D D f x y d g x y d 特殊地 ( , ) ( , ) .    D D f x y d f x y d 则有 f (x)  g(x) 性质５ 如果在 [a,b] 上 f x dx b a 则 ( ) g x dx b a  ( ) 特殊地 f x dx b a ( ) f x dx b a  ( )

性质6设M、m分别是f(x,y)在闭区域D上的 最大值和最小值，σ为D的面积，则 mo≤小f(x,y)do≤Mo (二重积分估值不等式) 性质7设函数f(化，y)在闭区域D上连续，o为D 的面积，则在D上至少存在一点（传，）使得 J∬fx,Jy)o=f(传，)o (二重积分中值定理)

山东农业大学 高等数学 主讲人：苏本堂 设M 、m分别是 f (x, y)在闭区域 D 上的 最大值和最小值， 为 D 的面积，则 性质６ 设函数 f (x, y)在闭区域D上连续， 为D 的面积，则在 D 上至少存在一点( ,)使得 性质７ （二重积分中值定理）       D m f (x, y)d M  f (x, y)d = f (,) D （二重积分估值不等式）

性质7设函数f(x,y)在闭区域D上连续， ·为D 的面积，则在D上至少存在一点(5，)使得 ∬f(x,y)o=f(5,n·o D 证：由性质6可知 m≤川nfx,ydo≤M 由连续函数介值定理，至少有一点(5，)∈D使 f(.n)=f(x.y)da 因此 f(x.y)do=f(.n)o

山东农业大学 高等数学 主讲人：苏本堂 证: 由性质6 可知, m f x y M D      ( , )d 1 由连续函数介值定理, 至少有一点  = D f f x y     ( , )d 1 ( , ) 使 因此 设函数 f (x, y)在闭区域D 上连续， 为D 的面积，则在 D 上至少存在一点( ,)使得 性质７  f (x, y)d = f (,) D