《高等数学》课程教学资源（PPT课件，下册）二重积分的概念和性质

第十章重积分 第一节 二重积分的概念和性质 二节 二重积分的计算法 三节 三重积分 第四节 重积分的应用 重积分 多元函数积分学 曲线积分 曲面积分

山东农业大学 高等数学 主讲人：苏本堂 第十章 重积分 第一节 二重积分的概念和性质 第二节 二重积分的计算法 第三节 三重积分 第四节 重积分的应用 多元函数积分学 重积分 曲线积分 曲面积分

第一节二重积分的概念和性质 问题的提出 二、二重积分的定义 三、二重积分的性质

山东农业大学 高等数学 主讲人：苏本堂 第一节 二重积分的概念和性质 三、二重积分的性质 一、问题的提出 二、二重积分的定义

山东农业大 本堂 1.曲边梯形的面积 f(飞) yf(x) 1分割 2近似 (以直代曲) ! △S:≈f(5:)△x 3求和 S≈∑f5:)△x, 分法越细，越接近精确值 a xi X2 Xi 5 ,Xi+1 Xn-1b

山东农业大学 高等数学 主讲人：苏本堂 xi xi+1 1 x i x2  1 分割 2 近似 (以直代曲) i i xi S  f ( ) 3 求和 y x o y=f (x) n−1 x =   n i i xi S f 1 ( ) a b . . 分法越细，越接近精确值 1. 曲边梯形的面积 f (i )

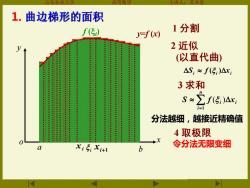
1.曲边梯形的面积 f(传) 1分割 y-=f() 2近似 : (以直代曲) △S:≈f(5:)△x 3求和 S≈】 f(5,)Ax, i=1 分法越细，越接近精确值 4取极限 X 5 令分法无限变细 i+1

山东农业大学 高等数学 主讲人：苏本堂 xi i xi+1  4 取极限 y x o y=f (x) 令分法无限变细 . a . b . . 分法越细，越接近精确值 1 分割 2 近似 (以直代曲) 3 求和 =   n i i xi S f 1 ( ) i i xi S  f ( ) 1. 曲边梯形的面积 . f (i )

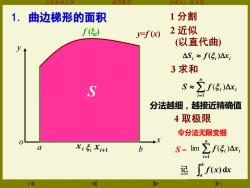
山东农业大 主讲人：苏本堂 1.曲边梯形的面积 1分割 f(传) yf(x) 2近似 (以直代曲) △S:≈f(5:)△x 3求和 S S≈∑f5:)△， i=1 分法越细，越接近精确值 4取极限 令分法无限变细 XiiXi+1 b S=lim f5)Ax, i=1 记 ["f(r)dx

山东农业大学 高等数学 主讲人：苏本堂 xi i xi+1  4 取极限 y x o y=f (x) 令分法无限变细 . . . . 分法越细，越接近精确值 1 分割 2 近似 (以直代曲) 3 求和 =   n i i xi S f 1 ( ) i i xi S  f ( ) 1. 曲边梯形的面积 . f (i ) =  n i i xi f 1 lim ( ) 记 S = .  b a f (x)dx S . a b

东液园 一、问题的提出 z=f(x,y) 1.曲顶柱体的体积 给定曲顶柱体： 底：xoy面上的闭区域D 顶：连续曲面z=∫(x,y)≥0 侧面：以D的边界为准线，母线平行于z轴的柱面 求其体积 问题：如何计算曲顶柱体的体积？

山东农业大学 高等数学 主讲人：苏本堂 问题： 如何计算曲顶柱体的体积？ 一、问题的提出 1.曲顶柱体的体积 给定曲顶柱体: 底： xoy 面上的闭区域 D 顶: 连续曲面 侧面：以 D 的边界为准线 , 母线平行于 z 轴的柱面 求其体积. D

山东农业大 高等数学 本 问题：如何计算曲顶柱体的体积？ =f(x,y 柱体体积=底面积关高 柱体体积=？ 特点：平顶. 特点：曲顶 解决问题的思路：类似定积分解决问题的思想： 分割，近似，求和， 取极限

山东农业大学 高等数学 主讲人：苏本堂 柱体体积=底面积×高 特点：平顶. 柱体体积=？ 特点：曲顶. z = f (x, y) D 问题： 如何计算曲顶柱体的体积？ “分割, 近似, 求和, 取极限” 解决问题的思路: 类似定积分解决问题的思想: ×

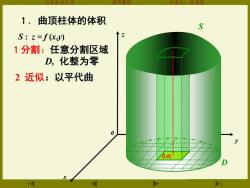
1.曲顶柱体的体积 S S:z=f(xy) 1分割：任意分割区域 D,化整为零 2近似：以平代曲 0 河

山东农业大学 高等数学 主讲人：苏本堂 x 0 z y D S S : z = f (x,y) １分割：任意分割区域 D, 化整为零 2 近似：以平代曲 １. 曲顶柱体的体积 i

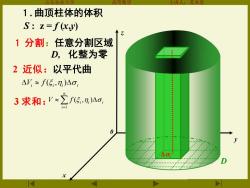
山东农业大 主讲人：本堂 1.曲顶柱体的体积 S:z=f(xy) 1分割：任意分割区域 D,化整为零 2近似：以平代曲 △V≈f(5,7,)△o 3求和：V≈∑f5,)△o 0 .△g

山东农业大学 高等数学 主讲人：苏本堂 x 0 z y D S : z = f (x,y) i i i i V  f ( , ) 3 求和： =   n i i i i V f 1 ( , )  2 近似：以平代曲 １ 分割：任意分割区域 D, 化整为零 . i １. 曲顶柱体的体积

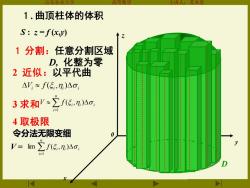
东液 1.曲顶柱体的体积 S:z=f(xy) 1分割：任意分割区域 D,化整为零 2近似：以平代曲 △V≈f(5,7,)△o 3求和'≈∑f,n)△o 4取极限 令分法无限变细 V=lim∑f5,n,)△o, i=1

山东农业大学 高等数学 主讲人：苏本堂 x 0 z y D S : z = f (x,y) i i i i V  f ( , ) 3 求和 =   n i i i i V f 1 ( , )  4 取极限 令分法无限变细 i 2 近似：以平代曲 １ 分割：任意分割区域 D, 化整为零 . =  n i i i i f 1 V = lim ( , )  １. 曲顶柱体的体积