《高等数学》课程教学资源（PPT课件，下册）格林公式及其应用

第三节格林公式及其应用 一、格林公式 二、平面上曲线积分与路径无关的条件 三、二元函数的全微分求积 四、全微分方程

山东农业大学 高等数学 主讲人：苏本堂 第三节格林公式及其应用 一、格林公式 二、平面上曲线积分与路径无关的条件 三、二元函数的全微分求积 四、全微分方程

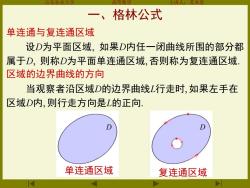
高等数学 本 格林公式 单连通与复连通区域 设D为平面区域，如果D内任一闭曲线所围的部分都 属于D,则称D为平面单连通区域，否则称为复连通区域 区域的边界曲线的方向 当观察者沿区域D的边界曲线L行走时，如果左手在 区域D内，则行走方向是L的正向. 单连通区域 复连通区域

山东农业大学 高等数学 主讲人：苏本堂 一、格林公式 单连通与复连通区域 区域的边界曲线的方向 当观察者沿区域D的边界曲线L行走时 如果左手在 区域D内 则行走方向是L的正向 单连通区域 复连通区域 设D为平面区域 如果D内任一闭曲线所围的部分都 属于D 则称D为平面单连通区域 否则称为复连通区域

格林公式 定理一设闭区域D由分段光滑的曲线L围成，函数 P(x,y)及Q(x,y)在D上具有一阶连续偏导数，则有 尝黔fP+w, D 或 dxdy=Pdx+Qdy 其中L是D的取正向的边界曲线， 注： 对复连通区域D,格林公式右端应包 括沿区域D的全部边界的曲线积分，且边 界的方向对区域D来说都是正向

山东农业大学 高等数学 主讲人：苏本堂   = +   −   L D dxdy Pdx Qdy y P x Q ( )  定理一 设闭区域D由分段光滑的曲线L围成函数 P(x y)及Q(x y)在D上具有一阶连续偏导数 则有 其中L是D的取正向的边界曲线 注: 对复连通区域D格林公式右端应包 括沿区域D的全部边界的曲线积分且边 界的方向对区域D来说都是正向 一、格林公式    = +    D L x y x y P x Q y P Q 或 d d d d

山东农业大 主计 苏本堂 证明：1)若D既是X-型区域，又是Y-型区域，且 D p1(x)≤y≤p2(x) . a≤x≤b d 41y)≤x≤Ψ2(y) B c≤y≤d 则ud=aw4 o a bx =∫w2yy)dy-∫wy,y)dy =∫cQ(x,y-∫aQ(x,d =jcBQ(x,yiy+jEac(x

山东农业大学 高等数学 主讲人：苏本堂 证明: 1) 若D 既是 X - 型区域 , 又是 Y - 型区域 , 且        a x b x y x D ( ) ( ) : 1  2 则 x y x Q D d d     = d c Q( ( y), y )dy  2   ( )  ( ) 2 1 d y y x x  Q   = CBE Q(x, y)dy  + EAC Q(x, y)dy  − d c Q( ( y), y )dy 1  = d c dy d c y o x E C A B a b D

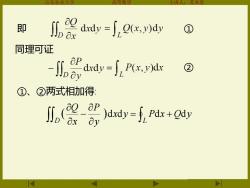
即 j2at-j.e,t ① 同理可证 ,那dha-j,P. ② ①、②两式相加得 n9d手ua

山东农业大学 高等数学 主讲人：苏本堂 即 同理可证 ① ② ①、②两式相加得: ( )   = +   −   D L x y P x Q y y P x Q d d d d

2)若D不满足以上条件，则可通过加辅助线将其分割 为有限个上述形式的区域，如图 ,影at n9Na = -jmPd+Ody(aD:表示D,的正向边界) k=1 Pdx+Qdy 证毕

山东农业大学 高等数学 主讲人：苏本堂 y o x L 2) 若D不满足以上条件, 则可通过加辅助线将其分割 D1 Dn D2  ( )  =   −   = n k D x y y P x Q k 1 d d ( ) x y y P x Q D d d   −     =  = + n k Dk P x Q y 1 d d  = + L Pdx Qdy 为有限个上述形式的区域 , 如图 ( 表示 的正向边界) Dk Dk  证毕

格林公式 dxdy=fPdx+Qdy 1 推论：正向闭曲线L所围区域D的面积 A=2手，dy-yd 例，稀圆L80038s2r所西面羽 A-ifrdy-vdx (abcosb

山东农业大学 高等数学 主讲人：苏本堂 推论: 正向闭曲线 L 所围区域 D 的面积  = − L A xdy y dx 2 1 格林公式    = +        −   D L x y P x Q y y P x Q d d d d 例如, 椭圆     , 0 2 sin cos :      = = y b x a L 所围面积  = +     2 0 2 2 ( cos sin )d 2 1 ab ab =  ab

山东农业才 本堂 格林公式的应用 1.简化二重积分 例1.计算 e dxdy,其中D是以O(0,0),A(1,1), B(0,1)为顶点的三角形闭域. 解：令P=0,Q=xey,则 =e-v2 ao ap B(0,1) A(1,1) 8x Oy D 利用格林公式，有 y=x Seddyfxedy =joxe"dy=j0edl-e〉

山东农业大学 高等数学 主讲人：苏本堂 格林公式的应用 1. 简化二重积分 例1. 计算 其中D 是以 O(0,0) , A(1,1) , B(0,1) 为顶点的三角形闭域 . 解: 令 , 则 2 0, y P Q xe − = = 利用格林公式, 有  − = D y x e dy 2 x e y OA y d 2  − = ye y y d 1 0 2  − = (1 ) 2 1 −1 = − e y = x o y x A(1,1) B(0,1) D

2.简化曲线积分 例2.设L是一条分段光滑的闭曲线，证明 2xydx+x2dy=0 证：令P=2xy,9=x2,则 80 ap Ox Oy =2x-2x=0 利用格林公式，得 f2xydx+x2dy=fodxdy=0

山东农业大学 高等数学 主讲人：苏本堂 2. 简化曲线积分 例2. 设 L 是一条分段光滑的闭曲线, 证明 2 d d 0 2 + =  xy x x y L 证: 令 2 , , 2 P = xy Q = x 则 利用格林公式, 得 xy x x y L 2 d d 2  +  = D 0dx dy = 0

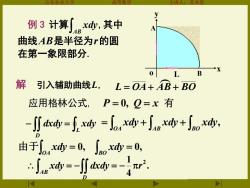
本堂 例3计算∫ex,其中 曲线AB是半径为r的圆 在第一象限部分. 0 B 解 引入辅助曲线L,L=OA+B+BO 应用格林公式，P=0,Q=x有 ∬=fx=o+6+ao, 由于o4x=0,∫ox=0, ∫sw=-J∬k=-4r2

山东农业大学 高等数学 主讲人：苏本堂 例 3 计算AB xdy,其中 曲线AB是半径为r的圆 在第一象限部分. 解 引入辅助曲线L, L = OA+ AB + BO 应用格林公式, P = 0, Q = x 有   − = L D dxdy xdy ,    = + + OA AB BO xdy xdy xdy x y o L A B = 0, = 0, OA BO 由于 xdy xdy . 4 1 2 xdy dxdy r D AB  = − = −   