《高等数学》课程教学资源（PPT课件，下册）多元函数的基本概念

山东农大号 第九章多元函数微分法及其应用 第一节 多元函数的基本概念 第二节 偏导数 第三节 全微分 第四节 多元复合函数的求导法则 第五节 隐函数的求导公式 第六节 多元函数微分学的几何应用 第七节 方向导数与梯度 第八节 多元函数的极值及其求法

山东农业大学 高等数学 主讲人：苏本堂 第九章 多元函数微分法及其应用 第一节 多元函数的基本概念 第二节 偏导数 第三节 全微分 第四节 多元复合函数的求导法则 第五节 隐函数的求导公式 第六节 多元函数微分学的几何应用 第七节 方向导数与梯度 第八节 多元函数的极值及其求法

第一节多元函数的基本概念 一、 平面点集 n维空间 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性

山东农业大学 高等数学 主讲人：苏本堂 一、平面点集 n维空间 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性 第一节 多元函数的基本概念

一、 平面点集 n维空间 1.平面点集 坐标平面上具有某种性质P的点的集合，称为平面点 集，记作 E={(x,y川(x,y)具有性质P}: 例如，平面上以原点为中心、为半径的圆内所有点 的集合是 C={(x,y)x2+y2<r2,C=(POP<r). 其中P表示坐标为(x,y)的点，OP表示点P到原点O的距离

山东农业大学 高等数学 主讲人：苏本堂 一、平面点集 n维空间 1.平面点集 坐标平面上具有某种性质P的点的集合 称为平面点 集记作 E={(x y)| (x y)具有性质P} 例如 平面上以原点为中心、r为半径的圆内所有点 的集合是 C={(x y)| x 2+y 2<r 2} 或C={P| |OP|r} 其中P表示坐标为(x y)的点 |OP|表示点P到原点O的距离

2.邻域 点集U(P,δ)={P|PPo<⊙，称为点P的δ邻域. 例如，在平面上， U(P,δ)={《x,y)V(x-xo)2+(y-o)2<δ圆邻域) 说明：若不需要强调邻域半径δ，也可写成U(P) 点P的去心邻域记为U(P)={P0<PP<δ} 在讨论实际问题中也常使用方邻域，因为方邻域与圆 邻域可以互相包含 平面上的方邻域为 U(Po,δ)={(x,y)x-xo<δ，y-yo<δ}

山东农业大学 高等数学 主讲人：苏本堂 0 δ  PP0  2. 邻域 点集 称为点 P0 的邻域. 例如,在平面上, U ( P0 ,δ ) = (x, y)  (圆邻域) 说明：若不需要强调邻域半径 ,也可写成 ( ). U P0 点 P0 的去心邻域记为 δ PP0  在讨论实际问题中也常使用方邻域, 平面上的方邻域为 U(P0 ,δ ) = (x, y)  因为方邻域与圆 邻域可以互相包含

3.内点外点边界点 内点：如果存在点P的某一邻域UP), 使得U(P)cE,则称P为E的内点； 外点 边界点 外点：如果存在点P的某个邻域 UP),使得U(P)E=O,则称P为E的 外点； 边界点：如果点P的任一邻域内既有 内点 属于E的点，也有不属于的点，则称P 点为E的边点 聚点如果对于任意给定的0，点P的去心邻域U(P,6)内总 有E中的点，则称P是E的聚点

山东农业大学 高等数学 主讲人：苏本堂 3.内点 外点 边界点 •内点 如果存在点P的某一邻域U(P) 使得U(P)E 则称P为E的内点 •外点 如果存在点 P的某个邻域 U(P) 使得U(P)E= 则称P为E的 外点 •边界点 如果点P的任一邻域内既有 属于E的点 也有不属于E的点 则称P 点为E的边点    边界点 内点 外点 聚点 如果对于任意给定的0 点 P 的去心邻域U(P, )  内 总 有E中的点 则称P是E的聚点

导效 方本 4.开区域及闭区域 ·若点集E的点都是内点，则称E为开集； ·E的边界点的全体称为E的边界，记作∂E, ·若点集E一OE,则称E为闭集； ·若集D中任意两点都可用一完全属于D的折线相连 则称D是连通的； ·连通的开集称为开区域，简称区域； ·开区域连同它的边界一起称为闭区域

山东农业大学 高等数学 主讲人：苏本堂 D 4. 开区域及闭区域 • 若点集 E 的点都是内点，则称 E 为开集； • 若点集 E E , 则称 E 为闭集； • 若集 D 中任意两点都可用一完全属于 D 的折线相连 , • 开区域连同它的边界一起称为闭区域. 则称 D 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; 。 。 • E 的边界点的全体称为 E 的边界, 记作E ;

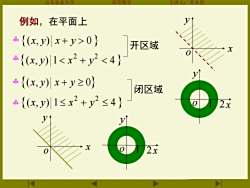
例如，在平面上 {(xy)x+y>0} 开区域 {(x,y)1<x2+y2<4} 1 {(,y)x+y≥0} 闭区域 {(x,y)1≤x2+y2≤4} 2x 2x

山东农业大学 高等数学 主讲人：苏本堂 例如，在平面上 (x, y) x + y  0  ( , ) 1 4  2 2 x y  x + y  (x, y) x + y  0 ( , ) 1 4  2 2 x y  x + y  开区域 闭区域     x y o 1 2 x y o x y o x y o 1 2

主计 苏本堂 整个平面是最大的开域， 也是最大的闭域； 点集{(x,y)川x>}是开集， 但非区域 ·对区域D,若存在正数K,使一切点P∈D与某定点 A的距离AP飞K,则称D为有界域，否则称为无 界域

山东农业大学 高等数学 主讲人：苏本堂  整个平面  点集 (x, y) x  1 是开集， 是最大的开域 , 也是最大的闭域； 但非区域 . −1 o 1 x y • 对区域 D , 若存在正数 K , 使一切点 PD 与某定点 A 的距离 AP K , 则称 D 为有界域 , 界域 . 否则称为无

5.n维空间 n元有序数组(1，x2,.,xn)的全体称为n维空间， 记作R”,即 Rn=RxRX.xR ={(,2,.,xnk∈R,k=1,2,.,n} n维空间中的每一个元素(x1,x2,.,xn)称为空间中的 一个点，数x称为该点的第k个坐标 当所有坐标x=0时，称该元素为R”中的零元，记作

山东农业大学 高等数学 主讲人：苏本堂 5. n 维空间 n 元有序数组 的全体称为 n 维空间, R , n n 维空间中的每一个元素 称为空间中的 称为该点的第k 个坐标 . 记作 即 R = R R R n 一个点, 当所有坐标 称该元素为 n R 中的零元,记作 O

R”中的点x=(x1,x2,.,xn)与点y=(y1,y2,.,yn) 的距离记作p(x,y)或x-y,规定为 px,y)=V(x-)2+(2-y2)2+.+(xn-yn)2 R"中的点x=(,x2,.,x)与零元O的距离为 x=yx好+号++x场 当n=1,2,3时，x通常记作x. R"中的变元x与定元a满足x-ad→0记作x→a. Rm中点a的8邻域为 U(a,δ)={xx∈R",p(x,a<δ}

山东农业大学 高等数学 主讲人：苏本堂 的距离记作 中点 a 的  邻域为 ( , , , ) 1 2 n R ( , , , ) 与点 y = y y  y 1 2 n n中的点x = x x  x 规定为 R ( , , , ) 1 2 n n中的点x = x x  x 与零元 O 的距离为 2 2 2 2 1 n x = x + x ++ x 当n =1,2,3时, x 通常记作 x . R x a x − a → 0 n中的变元 与定元 满足 记作 x → a. n R