《概率论与数理统计》课程教学资源（PPT课件）6.3 统计量及其分布（简）

第三节抽样分布 如何利用样本对总体进行统计推断？一针对不同问题 构造适当的样本函数 一、统计量 *一、经验分布函数 三、抽样分布 四、四个重要定理

一、统计量 *二、经验分布函数 三、抽样分布 四、四个重要定理 第三节 抽样分布 如何利用样本对总体进行统计推断？——针对不同问题 构造适当的样本函数

一、统计量 定义设X,X2,X,n是来自总体X的一个样本， g(X1,X2,Xn)是X1,X2,X,的函数，若g中不含未知参 数，则称g(X,X2,Xm)是一统计量. 若g中含未知参数，则称g(X1,X2,Xn)是枢轴量. 例.X~N(μ，o2),山，o2是未知参数，X1,X2,Xn是 来自总体X的一个样本 x2x.s是2(x-对 统计量 寻2(x-川不是统计量.若4a已知，则为统计立

一、统计量 定 义 设 1 2 , , , X X Xn 是来自总体 X 的一个样本 , 1 2 ( , , , ) n g X X X 是 1 2 , , , X X Xn 的函数，若 g 中不含未知参 数，则称 1 2 ( , , , ) n g X X X 是一统计量. —— 统计量. 1 1 , n i i X X n = =  ( ) 2 2 1 1 1 n i i S X X n = = − −  ( ) 2 2 1 1 n i i X   =  − 不是统计量. 若, 已知,则为统计量. 若g中含未知参数，则称 枢轴量. 1 2 ( , , , ) n g X X X 是 2 2 1 2 ~ ( , ) , , , , , . X N X X Xn X     是未知参数， 是 来自总体 的一 例 个样本

几个常见统计量：设X,X,X是来自总体X的一个样本， x1,x2,.,x,是这一样本的观察值. ①样本平均值：=1∑X 2样本方差：s,2x-x,(2-n 样本标准差：S=vS=2(X-广-石 8)样本k阶原点矩：A=之X,k-12, X,= (④)样本k阶中心矩： 4,=1∑X B=1(X,-),k=2,3,. n一 A2x-0=2-x→4

几个常见统计量： 1 2 1 2 , , , X , , , n n X X X x x x 设 是来自总体 的一个样本， 是这一样本的观察值. (1)样本平均值: 1 1 . n i i X X n = =  (2)样本方差: 2 2 1 1 ( ) 1 n i i S X X n = = − −  2 2 1 1 . 1 n i i X nX n =   = −   −    样本标准差: ( ) 2 2 1 1 . 1 n i i S S X X n = = = − −  (3)样本 k 阶(原点)矩: 1 1 , 1, 2, . n k k i i A X k n = = =  (4)样本 k 阶中心矩: 1 1 ( ) , 2, 3, . n k k i i B X X k n = = − =  2 2 1 1 ( ) n i i B X X n = = −  2 2 1 1 n i i X X n = = −   1 1 2 2 1 1 1 n i i n i i A X X n A X n = = = = =  2 A A B 2 1 2 − =

它们的样本观察值分别为 -I2* 2s-=2m月 -是2-=品2四m a滑2，=12 6-2x-,k=2,3

1 1 ; n i i x x n = =  1 1 , 1,2, ; n k k i i a x k n = = =  1 1 ( ) , 2,3, . n k k i i b x x k n = = − =  2 2 1 1 ( ) 1 n i i s x x n = = − −  2 2 1 1 ; 1 n i i x nx n =   = −   −    2 1 1 ( ) 1 n i i s x x n = = − −  2 2 1 1 ( ); 1 n i i x nx n = = − −  它们的样本观察值分别为

样本矩与总体矩的关系 A4-2x5,k=1,2,n 定理如果总体X的k阶原点矩E(X)=4存在，则当n→o时， (1)AP→4，k=1,2,L 矩估计法的理论根据 (2)若g是连续函数，则g(A1,4,4)声pg(4,山，4) 证明：(1)因为X(i=1,2,.)独立同分布， E(4)=EX)=2E(x)=4 i1 由辛铁大数定理可得艺X一4 (2)由依概率收敛的序列的性质(P120)可得. 因此，可以用样本矩估计相应的总体矩；用样本矩的连续 函数估计相应的总体矩的连续函数， *二、经验分布函数

矩估计法的理论根据 1 1 , 1, 2, , . n k k i i A X k n n = = =  *二、经验分布函数 因此，可以用样本矩估计相应的总体矩；用样本矩的连续 函数估计相应的总体矩的连续函数. 1 ( 1, 2, .) k （ ）因为X i i = 独立同分布， （2）由依概率收敛的序列的性质（P120）可得. 证明： 由辛钦大数定理可得 1 1 ( ) ( ) k n k i i E A E X n = =  1 1 ( ) n k k i E X n  = = =  1 1 k n i i X n =  P ⎯⎯→k （2）若g是连续函数，则 ( ) k X E X k 定理 如果总体 的k阶原点矩 = →   存在，则当n 时， 1 , 1, 2, P （ ）A k k k ⎯⎯→ =  L 1 2 1 2 ( , , , ) ( , , , ) P k k g A A A g ⎯⎯→    样本矩与总体矩的关系

三、抽样分布 统计量服从的分布称为抽样分布， 要求：牢记三大分布的定义、性质、密度函数图形轮廓； 并能够查表计算。 (一)X分布设X,X2,Xn是来自总体N0,)的一个样本， 则称统计量x=X?+X好+.+X为服从自由度为n的x分布， 记为x2~x()。自由度指定义式中包含的独立变量的个数. f(y)1 概率密度为 n=1 n=4 ye,y>0 f0)=2r n=10 0 其它 随着的增大，密度曲线逐渐趋于平缓、对称

三、抽样分布 统计量服从的分布称为抽样分布. 2 （一） 分布 设 1 2 , , , X X Xn 是来自总体 N(0,1) 的一个样本， 则称统计量 2 2 2 2  = + + + X X X 1 2 n 为服从自由度为 n 的 2  分布， 记为 2 2   ~ ( ) n 。自由度 指定义式中包含的独立变量的个数. 1 2 2 2 1 0 ( ) . 2 ( ) 2 0 n y n y e y n f y  − −    =     ， 其它 概率密度为 n = 1 随着n的增大，密度曲线逐渐趋于平缓、对称. 要求：牢记三大分布的定义、性质、密度函数图形轮廓； 并能够查表计算. y f y( )O n = 4 n = 10

x分布的性质 性质1（x分布的可加性) 设x~x2(n),~x2(2),并且，x3独立， 则+x2x2(n1+n2). (此性质可以推广到多个随机变量的情形) 设x~X2(n,),并且X(i-1,2,m)相互独立， 则∑x若x+%++

性质1 (此性质可以推广到多个随机变量的情形) 2  分布的性质 2 2 2 2 2 1 2 1 ~ ( ), ( 1, 2, , ) , ~ ( ). i i i m i m i n i m n n n      = =  + + + 设 并且 相互独立 则 2 2 2 2 2 2 1 1 2 2 1 2 2 2 2 1 2 1 2 ~ ( ), ~ ( ), , , ~ ( ). n n n n          + + 设 并且 独立 则 2 ( )  分布的可加性

eaa=oir 性质2(X分布的数学期望和方差) (a>0,0>0) 若xX2~x2(n,则E(x2)=n,D(x)=2n. 证明：x2-X+X+.+X7,其中X,~N0,1), E(X)=DX)+E2(X)=1, x分布的定义式 D(X,)=EX-E(X,=3-1=2,i=1,2,n -2对时-芝2ar Dr=o2x2-a2}2r}=

性质2 证明： ~ (0, 1), 其中X N i 2 2 ( ) ( ) ( ) E X D X E X i i i = + 2 4 2 2 ( ) ( ) [ ( )] D X E X E X i i i = − i n = 1, 2, , . 2 2 1 ( ) n i i E E X  =    =      2 1 ( ) n i i E X = =  = n, 2 2 1 ( ) n i i D D X  =   =      2 1 ( ) n i i D X = =  = 2 . n = − = 3 1 2, 2 2 2 2  = + + + X X X 1 2 n， 2 = 1,  分布的定义式 2 1 2 0 ( 0, 1 d ( ), 2 0) 2 t t e t         − −    =  2 1 4 2 d 2 t t e t   − − ( ) 5 2 1 5 2 2 3 2 2 2 =     = 2 ( )  分布的数学期望和方差 2 2 2 2 若   ~ ( ), n 则E n D n ( ) , ( ) 2 .   = =

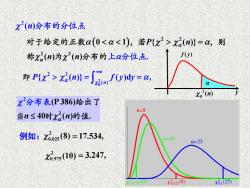
X(n)分布的分位，点 对于给定的正数a(0x2(m)}=a,则 称x2(n)为x(n)分布的上a分位，点. f(y) 即Px>2ay=是fU山=a Xa(n) x2分布表(P386)给出了 n=8 当n≤40时x2(n)的值. 例如：x602s(8)=17.534, h=25 x695(10)=3.247, 0.97510 Xi02s(8) X61(25)

( ) 2 2 2 2 0 1 { ( )} ( ) ( ) . P n n n          对于给定的正数    = ，若 ，则 称 为 分布的上 分位点  y f y( ) 2  ( ) n 分布的分位点 2 2 2 ( ) { ( )} ( )d , n P n f y y       +  = = 即  例如： = 17.534, 2 0.025  (8) 2 0.975  (10) = 3.247, 2 2 (P 386) n n 40 ( ) .     给出了 当 时 布表 的值 分 2   ( ) n

费希尔(R.A.Fisher)证明了： 当n充分大时，店0+2m-i 其中乙a是标准正态分布的上a分位点. 利用上述公式，可以求得n>40时，上分位，点的近似值. 例如s(50≈，(s+V2x50-) 165+v网=6721 而查详表可得X6.s(50)=67.505

例如 = 67.221. 利用上述公式, 而查详表可得 2 0.05  (50) 67.505 . = 费希尔(R.A.Fisher)证明了: 2 2 1 ( ) ( 2 1) . 2 , . n n z n z      当 充分大时  + − 其中 是标准正态分布的上 分位点 可以求得 40 , . n  时 上 分位点的近似值 2 2 0.05 0.05 1 (50) ( 2 50 1) 2   +  − z 1 2 (1.645 99) 2 = +