山东理工大学：《线性代数》课程教学课件（PPT讲稿）第二章 矩阵与向量 2-3 向量组的线性相关性

©山本理上大军 第三草包黨的线性相关性 一、线性组合 二、方程组矩阵向量组的关系 三、 向量组的线性相关性 四、向量组的秩 五、向量空间的维数 返回

四、向量组的秩 一、线性组合 三、 向量组的线性相关性 五、向量空间的维数 二、方程组 矩阵 向量组的关系

©山本理工大军 课前复习 1、定义n个数41,42，.，4n组成的有序数组 a=(a1a2.an 称为一个n维向量，其中a,称为第i个分量（坐标). n维向量写成一行称为行向量， n维向量写成一列称为列向量： 2、几种特殊向量 实向量，复向量，零向量，单位向量，向量同型 士向量相降 工王王

课前复习 １、定义 ｎ个数 a a a 1 2 , , , n 组成的有序数组  = (a a a 1 2 n ) 称为一个ｎ维向量，其中 称为第 个分量（坐标）. i a i ｎ维向量写成一行称为行向量， ｎ维向量写成一列称为列向量. ２、几种特殊向量 实向量，复向量，零向量，单位向量，向量同型， 向量相等

©少本理二大 王 4、向量的运算 5、向量组 若干个同维数的列向量（或同维数的行向量)所 组成的集合叫做向量组 6、向量空间 设V为n维非空向量组，且满足 ①对加法封闭 ifa∈'V,B∈V→a+B∈V; ②对数乘封闭 fa∈V,入∈R→a∈V. 那么就称集合V为向量空间！

若干个同维数的列向量（或同维数的行向量）所 组成的集合叫做向量组． ５、向量组 if V V V        +  , ; ６、向量空间 设Ｖ为ｎ维非空向量组，且满足 ①对加法封闭 ②对数乘封闭 那么就称集合Ｖ为向量空间. if V R V        , . ４、向量的运算

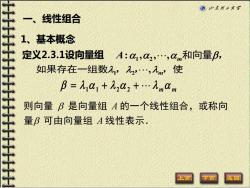
©山本理工大军 一、线性组合 1、基本概念 定义2.3.1设向量组A:a1,a2,0n和向量B, 如果存在一组数21，入2，入m使 B=1a1+12a2+.九nm 则向量B是向量组A的一个线性组合，或称向 量B可由向量组A线性表示

1、基本概念 定义2.3.1设向量组 A:1 ,2 ,  , m 和向量，  =  1  1 +  2  2 +   m  m 则向量  是向量组 A 的一个线性组合，或称向 量 可由向量组 A 线性表示． 如果存在一组数1 ，2 ， ,m ，使 一、线性组合

⊙中本理工大军 相关知识点 例1：任一n维向量a=（a,a2.an)都是 n维单位坐标向量组 e=(10.0)62=(01.0), 6=(00.1),的一个线性组合. 显然有 a=a181+a2E2+.+nen 注： ①零向量O是任一向量组的线性组合· O=0a1+0a2+.+0am ②向量组中每一向量都可由该向量组线性表示 a2=0a1+1a2+0a3+.+0am 回

① 零向量Ｏ是任一向量组的线性组合． ② 向量组中每一向量都可由该向量组线性表示． 1 2 0 0 0 . O = + + +    m ( ) 1  = 1 0 0 ， ( ) 2  = 0 1 0 ， ， (0 0 1) n  = ， 例1：任一ｎ维向量  = (a a a 1 2 n ) 都是 的一个线性组合． 1 1 2 2 . n n 显然有     = + + + a a a n 维单位坐标向量组 注： 2 1 2 3 = + + + + 0 1 0 0 .      m

©P本理工大军 例2：证明向量ax(04,2)是向量ax(1,2,3)a(2,3,1), a3,1,2)的线性组合，并将o用a1,az2,a3 线性表示 解：先假设a=1ax+22a2十入3a3,即 (0,4,2=入1,2,3开22(2,3,1t23(3,1,2) λ十2兄2十323=0 123 因此 {2十32+2=4 由于 231=18≠0 3九+兄2+222 312 所以方程组有唯一解，可得入1，入21，入=一1， 于是 0=a1+a2a3

例2: 证明向量 ＝(0，4，2) 是向量 (1 2 3) (2 3 1) 1 ＝ ，2 ＝ ， 3 ＝(3，1，2)， 的线性组合, 并将 1 2 3 用 , , 线性表示 解: 先假设 ＝1 1 ＋2  2 ＋3  3 ， 即 (0 4 2) (1 2 3) (2 3 1) (3 1 2) ，＝1 ，＋2 ，＋3 ，      3 2 2 2 3 4 2 3 0 1 2 3 1 2 3 1 2 3 ＋ ＋ ＝ ＋ ＋ ＝ ＋ ＋ ＝          因此 由于 18 0 3 1 2 2 3 1 1 2 3 ＝ －  所以方程组有唯一解,可得 1 ＝1，2 ＝1，3 ＝ －1， 于是 ＝1 ＋2 －3

小结： a与a1,a2,am的关系为以下三种情院一： 1、a可由a1,a2,.,am线性表示，且表达式唯一， 2a可由a1,&2,an线性表示，但不唯一 如0,0)=(4，-1)+(1,1)=01，-1)+0(-1,1) 3不能由a1,a2,am线性表示 回

小结: , , , : 与1  2   m 的关系为以下三种情形之 一 1、 可 由1 , 2 ,  , m 线性表示， 且表达式唯一； 2、 可 由1 , 2 ,  , m 线性表示， 但不唯一， 如(0, 0) = (1, −1)+ (−1,1) = 0(1, −1)+ 0(−1,1) 3、 不能由1 ,2 ,  , m 线性表示

二、元线性方程组、矩阵、向量组的关系 若干个同维数的列向量（或同维数的行向量）所组 成的集合叫做向量组， 例如：矩阵A=(amxm有n个m维列向量： 11 12 A- 21 L22 2n mj 向量组a1,2,an称为矩阵A的列向量组

向量组α1 , α2 ,···, αn称为矩阵A的列向量组. 若干个同维数的列向量(或同维数的行向量)所组 成的集合叫做向量组. 例如: 矩阵A=(aij)mn有n个m维列向量:             = a a a a a a a a a a a a m m mj mn j n j n A             1 2 21 22 2 2 11 12 1 1 1  2  j  n 二 、 n元线性方程组、 矩 阵、 向量组的关系

类似地，矩阵A-(amxn有n个n维行向量： 402122 a2n a, A= a402 a aml am2 向量组a,a必，am称为矩阵A的行向量组. 上页 回

                = a a a a a a a a a a a a m m mn i i in n n A             1 2 1 2 21 22 2 11 12 1 1  向量组1 ’ , 2 ’ ,···, m ’称为矩阵A的行向量组. 类似地, 矩阵A=(aij)mn有m个n 维行向量: 2  i   m 

线性方程组的向量表示 12 L211 22 因此线性方程组可写为 a1x1+02x2+.+0nxn=B 于是方程组有没有解的问题转化为向量B能否由 向量组01，C2,:,0n线性表示 王

线性方程组的向量表示        + + + = + + + = + + + = m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b         1 1 2 2 21 1 22 2 2 2 11 1 12 2 1 1     1 1 2 2 n n x x x + + + = 1  2  n  因此线性方程组可写为 方程组有没有解的问题转化为向量  能否由 向量组 线性表示. 1 2    , , , n 于是