山东理工大学：《线性代数》课程教学课件（PPT讲稿）第三章 矩阵的运算 3-3 初等矩阵

©山东理工大￥ 课前复习 逆矩阵对于n阶矩阵A,如果有一个n阶矩阵B, 使得 AB=BA=E, 则称矩阵A是可逆的，并把矩阵B称为A的逆矩阵 A的逆矩阵记作A. 说明若A是可逆矩阵，则A的逆矩阵是唯一的， 定理 矩阵A可逆的充要条件是10，且 4=- A,其中A为矩阵A的伴随矩阵 当A=0时，A称为奇异矩阵； 当A10时，A称为非奇异矩阵 2 上页 下页 返回}

课前复习 使得 的逆矩阵记作 逆矩阵 对于ｎ阶矩阵Ａ，如果有一个ｎ阶矩阵Ｂ， 则称矩阵Ａ是可逆的，并把矩阵Ｂ称为Ａ的逆矩阵. 说明 若Ａ是可逆矩阵，则Ａ的逆矩阵是唯一的. 定理 矩阵Ａ可逆的充要条件是 ，且 其中 为矩阵Ａ的伴随矩阵. 当 时，Ａ称为奇异矩阵； 当 时，Ａ称为非奇异矩阵

运算规律（设AB均是n阶方阵） ©山东理二大军 1)若A$PA'S,且（A)=A. 2)若S,110pUA)'s,且0A)'=4 3)若A'S,B1$,且A,B同阶，P(AB)S, 且(AB)=B1A 推广 (44LA)=4LAA. 4)若'sp(4)'s,且(4)=(4)、 5)若ASp4=4 T工

运算规律 （设ＡＢ均是ｎ阶方阵） 1）若 且 2）若 且 3）若 ，且 同阶， 推广 4）若 且 5）若 6）若 且 且

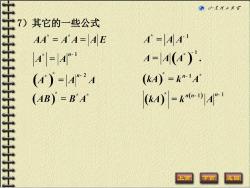
士 ©山东理工大￥ 7)其它的一些公式 AA=AA=AE A=4 4=A 4=4). (4)=AA (kA)=k"A (AB)=B'A (kA)=ka.少A- 上页 下页

7）其它的一些公式

©中本理工大军 第三节初等阵 一 初等矩阵 二基本结论 三应用举例 上页 区回

©出本理工大军 一、初等矩阵的概念 定义E4短P,P就称为初等矩阵 相应的，三种初等变换对应着三种初等方阵 1、对调 al 0 0 () 记作E(i,) g (c) (c) 上页 返回

相应的，三种初等变换对应着三种初等方阵. 一、初等矩阵的概念 定义 １、对调 就称为初等矩阵. 记作

山本理大军 12 M M M 安王二二二二王二十二二二二 E(i,j)A ÷ 0i2 L M M M M L a jn M M M (c) (c) L 2e11 012 L M S M ji ajz C jn () 交换两行相 C M S M M÷ 当于左乘矩 san 0m() 阵E6,) M M M÷ cam am2 L (mu

交换两行相 当于左乘矩 阵

山本理工大 2e0M11 L L L ain 6 L L ai L AE,(i,j)= M M M M L L L (c) 交换两列相当于右乘矩阵E,6,) 上页 回

交换两列相当于右乘矩阵

、 数乘 0 ( 记作E(i() (c 上页

２、数乘 记作

东置工大 L 0 0 L L L L L L .÷ E.(i(k))A= So L@ L L L a in L L L L L L 80 L 0 L 1 L L L M L M L ·÷ 上页 返回

©山本理工大军 2eu1 L M M E（ik)A-ha M M L e11 L kavi L AE,(i(k))=M M M L L (c)