《概率论与数理统计》课程教学资源（PPT课件）4.2 方差

第二节方差(Variance) 一、方差的定义 二、方差的性质 三、常见分布的方差 四、契比雪夫不等式

一、方差的定义 二、方差的性质 三、常见分布的方差 四、契比雪夫不等式 第二节 方差 (Variance )

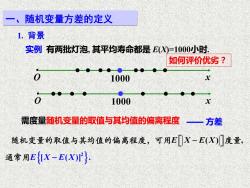
一、随机变量方差的定义 1.背景 实例有两批灯泡，其平均寿命都是E()=1000小时. 如何评价优劣？ 0 1000 x ● 1000 需度量随机变量的取值与其均值的偏离程度一—方差 随机变量的取值与其均值的偏离程度，可用E[X-E(X)川度量， 通常用E{K-E(X}

1. 背景 实例 有两批灯泡, 其平均寿命都是 E(X)=1000小时. • O x • • • • • • • • • O x • • • • • • • • • 1000 • 1000 一、随机变量方差的定义 如何评价优劣？ 需度量随机变量的取值与其均值的偏离程度 —— 方差 E X E X   − ( ) , 随机变量的取值与其均值的偏离程度，可用  度量   2 通常用E X E X [ ( )] . −

2.定义设X是一个随机变量，若E{LX-E(X)}存在，则称 ELX-E(X)}为X的方差，记为D(X)或Var(X),即 D(X)=Var(X)-Ex-E(X Variance 称√D(X)为标准差或均方差，记为σ(X). 注：方差刻划了随机变量的取值对于其数学期望的偏离程度。 方差一就是随机变量X的函数g(X)=[X-E(x)]的数学期望！

2. 定义 2 2 , {[ ( )] } , {[ ( ) ] } ( ) Var( ), X E X E X E X E X X D X X − − 方 设 是一个随机变量 若 存在 则称 为 的 差，记为 或 即 注：方差刻划了随机变量的取值对于其数学期望的偏离程度。 称 D( ) , X 为标准差或均方差 记为σ( ). X    2 D X X E X E X ( ) Var( ) ( ) . = = −   2 方差——就是随机变量X g X X E x 的函数 ( ) ( ) = − 的数学期望！ ( Variance )

定理1°设X为离散型随机变量，分布律为 P{X=x}=p(k=1,2,),若∑x-E(X)P k=1 绝对收敛，则D=2x-E(Xn. 2°设X为连续型随机变量，概率密度为f), 若∫Ix-E(X)f(x)dx绝对收敛，则 DX=∫Ix-E(X)Ff(x)dx

定理 1 o 设 X 为离散型随机变量，分布律为 { } ( 1,2, ) P X x p k = = = k k ，若 2 1 [ ( )] k k k x E X p  =  − 绝对收敛，则 2 1 ( ) [ ( )] k k k D X x E X p  = = −  。 2o 设 X 为连续型随机变量，概率密度为 f (x)， 若 2 [ ( )] ( )d x E X f x x  − −  绝对收敛，则 2 D X x E X f x x ( ) [ ( )] ( )d  − = − 

计算公式： D0=E)-EP重！1 证：DX=Ex-E(X'} =E{x2-2X.E(X)+[E(X)]} =E(X)-2E(X)·E(X)+[E(X)] =E(X2)-[E(X)]

计算公式：   2 D X E X E X ( ) ( ) = −    2 2 = −  + E X X E X E X 2 ( ) ( )  2 2 = −  + E X E X E X E X ( ) 2 ( ) ( ) ( )  2 2 = − E X E X ( ) ( ) 证： D X E X E X ( ) ( ) [ ( )] . = − 2 2 重要！！

例1设E(X)=4D(X)=o,求X=X二严的期望、方差. 解：(x)(。)=E(x-四-0 a-〔。]-月 =DX=1 ·.D(X）=E(x”)-[EX)]=1-02=1 X的标准化变量：x=X=4 推论：随机变量经过标准化后，期望和方差分别为0,1

2 例1 设E X D X ( ) ( ) = =   ， ，求 的期望、方差. X X    − = 解： ( ) X E X E      − =     ( ) 1 E X   = − = 0 ( ) 2 2 D X E X E X ( ) ( )     = −     2 X E      −         ( ) 2 2 1 E X   = −     2 1 D X( ) 1  =  = 推论： 随机变量经过标准化后，期望和方差分别为0,1. X X    − X的标准化变量： = 2 E X( )  = 2 = − = 1 0 1

二、方差的性质 1.设C是常数，则D(C)=0 证明D(C)=E(C2)-[E(C)=C2-C2=0. 2.设X是一个随机变量，C是常数，则有 D(CX)=C'D(X),D(X+C)=D(X) 证明D(Cx)=E{[Cx-E(Cx} -CEX-E(X)=C'D(X) D(X+C)-EX+C-E(X+CEX-E(XD(X) →D(aX+b)=dD(X)

证明 2 2 D C E C E C ( ) ( ) [ ( )] = − 二、方差的性质 2 2 = − C C = 0. 2. 设X C 是一个随机变量, 是常数,则有 证明 D CX ( )    2 2 = − C E X E X( ) 2 = C D X( ).    2 = − E CX E CX ( ) 1. ( ) 0 设C是常数，则D C = 2  + = D aX b a D X ( ) ( ) 2 D CX C D X ( ) ( ), = D X C D X ( ) ( ) + =    2 D X C E X C E X C ( ) ( ) + = + − +    2 = − = E X E X D X ( ) ( )

3.设X,Y是两个随机变量，则有 X,Y的协方差：COV(X,Y) D(X+Y)=D(X)+D(Y)+2EX-E(X)Y-E(Y) 特别地，当XY相互独立时，有D(X+Y)=D(X)+D(Y). 才证明：X1,X2,X相互独立，则 2y-交a2ogca 若x,Y独立，a,b是常数，则D(aX+bY)=D(X)+bD(Y) 4.D(X)=0的充要条件是P{X=E(X)}=1 证：(1)充分性：(=)若P{X=E(X)}=1. =PX2=E2X)}=1→E(X2)=E2(X) →D(X)=0. (2)必要性：（→）待证

D X Y D X D Y E X E X Y E Y ( ) ( ) ( ) 2 [ ( )][ ( )] + = + + − −   D X Y D X D Y ( ) ( ) ( ). + = + 3. 设X Y, 是两个随机变量,则有 特别地，当X,Y相互独立时，有 1 2 , , , 推 证明： 广：若X X Xn相互独立，则 2 1 1 ( ). n n i i i i i i D C X C D X = =   =       1 1 ( ), n n i i i i D X D X = =   =       若X ,Y 独立,a , b 是常数, 则 2 2 D aX bY a D X b D Y ( ) ( ) ( ) + = + 4. 0 { ( )} 1 D X P X E X ( ) = = = 的充要条件是 证： (1)充分性：( )  若 P X E X { ( )} 1. = = 2 2  = = P X E X { ( )} 1 2 2  = E X E X ( ) ( )  = D X( ) 0. (2)必要性： ( )  待证. X Y X Y , COV( , ) 的协方差:

DXE-EX X 01 三、常见分布的方差 Px 1-p p 1.两点分布：X~(0,1)参数为p.E(X)=p 例2 →DX)=PI-p 2.Poiss0n分布：X~π(2)，E(X)=元D(X)=元 例3 证PX=k=e,k=0,L2,>0 k! E(X)=E[X(X-1)+X]=E[X(X-1]+E(X) 含-哈4-心29*2 =2e.e2+1=22+:D(X)=E(X2)-[E(X)=2

三、常见分布的方差 1. ~ (0,1) . 两点分布：X p 参数为 例2  = − D X p p ( ) (1 ). X ~ ( )   ，E X （ ）=  { } , 0,1,2, , 0 ! k P X k e k k    − = = =  2. Poisson分布： D X （ ）=  例3 E X p （ ）=   2 E X E （ ）= X X （ − + 1） X ( ) 2 2 2 2 ! k k e k      − − = = + −  2 = +   0 ( 1) ! k k k k e k     − = = − +  = − + E X X E X  （ 1 ( ) ） 2 e e     − =  + 2 2  = − D X E X E X ( ) ( ) [ ( )] =  0 1 1 k X p p p − 证 2 2 D X E X E X ( ) ( ) [ ( )] = −

3.二项分布：X~b(n,p)E(X)=pDX)=pI-p)例6 方法1—一利用公式.记q=1-p. E(X)=E[X(X-I)+X]=E[X(X-1]+E(X) =∑kk-I)Cpq-*+np k=0 -2A-y+四 =2a4+即 台点(k-2)(n-k)! =n(u-1)pCip-+np=nn-Dp'+np. .D(X)=E(X2)-IE(X)月'=p(1-p)

3. ~ ( , ) 二项分布：X b n p E X np （ ）= 例 6   2 E X E X X X （ ）= − + （ 1） 0 ( 1) k k n k n k k k C p q np  − = = − +  = − + E X X E X  （ 1 ( ) ） 2 2  = − D X E X E X ( ) ( ) [ ( )] 2 ! !( ) ( ) ! 1 n k n k k k k p q np n k n k − = = − + − 2 ( 2)! ( 2)!( )! ( 1) n k n k k n k n n n p q k np − = = −− − + −  2 22 2 2 ( 1) n k n k k k n n p p q n Cn p −− − − = = − +  2 = − + n n p np ( 1) , = − np p (1 ) D X np p （ ）= − (1 ) 方法 1 —— 利用公式 . 记 q p = −1