《概率论与数理统计》课程教学资源（PPT课件）1.3 频率与概率

第三节频率与概率 讨论如何表征随机事件在一次试验中 发生的可能性的大小 频率 概率

第三节 频率与概率 ——讨论如何表征随机事件在一次试验中 发生的可能性的大小 频率 概率

一、频率 定义在相同的条件下，进行了n次试验，在这n次试验 中，事件A发生的次数n称为事件A发生的频数。比值4称 为事件4发生的颜率，并记成/4小，即人(4=一 基本性质： ()0≤f(A)≤1；(2)f(S)=1,f(0)=0; (3)若A,A2,A4是两两互不相容的事件，则 f(A UA,U.UA)=f(A)+(A)++(A)

定义 在相同的条件下，进行了 n 次试验，在这 n 次试验 中，事件 A 发生的次数nA 称为事件 A 发生的频数。 比值nA n 称 为事件 A 发生的频率，并记成 ( ) n f A 。 一、频率 (1) 0 ( ) 1; n   f A ( 2 ) ( ) 1, ( ) 0; f S f =  = (3) 若 1 2 , , , A A Ak是两两互不相容的事件，则 1 2 1 2 ( ) ( ) ( ) ( ) k n n n k f A A A f A f A f A = + + + 基本性质： 即 ( ) A n n f A n =

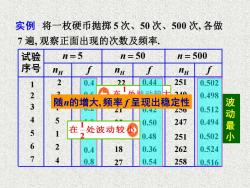
实例将一枚硬币抛掷5次、50次、500次，各做 7遍，观察正面出现的次数及频率， 试验 n=5 n=50 n=500 序号 na ng f ng f 1 2 0.4 22 0.44 251 0.502 0.498 3 随n的增大，频率f呈现出稳定性 U.4☑ Z50 0.512 4 5 0.50 247 0.494 5 1 在处波动较小 0.502 波动最小 0.48 251 6 2 0.4 18 0.36 262 0524 7 0.8 27 0.54 258 0.516

实例 将一枚硬币抛掷 5 次、50 次、500 次, 各做 7 遍, 观察正面出现的次数及频率. 试验 序号 n = 5 nH f 1 2 3 4 5 6 7 2 3 1 5 1 2 4 nH f n = 50 22 25 21 25 24 18 27 nH n = 500 251 249 256 247 251 262 258 0.4 0.6 0.2 1.0 0.2 0.4 0.8 0.44 0.50 0.42 0.48 0.36 0.54 f 0.502 0.498 0.512 0.494 0.524 0.516 0.50 0.502 在 处波动较大 2 1 在 处波动较小 2 1 波 动 最 小 随n的增大, 频率 f 呈现出稳定性

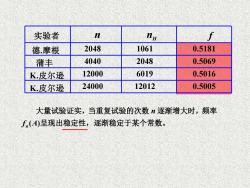
实验者 n Hu f 德摩根 2048 1061 0.5181 蒲丰 4040 2048 0.5069 K皮尔逊 12000 6019 0.5016 K皮尔逊 24000 12012 0.5005 大量试验证实，当重复试验的次数逐渐增大时，频率 f(A)呈现出稳定性，逐渐稳定于某个常数

实验者 德.摩根 蒲丰 K.皮尔逊 K.皮尔逊 n nH f 2048 1061 0.5181 4040 2048 0.5069 12000 6019 0.5016 24000 12012 0.5005 大量试验证实，当重复试验的次数 n 逐渐增大时，频率 ( ) n f A 呈现出稳定性，逐渐稳定于某个常数

例：计算机模拟抛掷骰子的试验 要求：输入实验次数，统计各点数(1~6点)出现的次数及频率， matlab模拟程序 function output args ]shaizi_sum(ntimes %设置随机发生器，取得随机数 rng('default'); x=rand(1,ntimes); %统计各点数出现的次数、频率 n_lp1=sum(x=1/6&x=2/6&x=3/6&x=4/6&x=5/6&x<=6/6); frequency =[n_Ip1,n_Ip2,n_Ip3,n_lp4,n_lp5,n_lp6]/ntimes; %输出结果 msg1=['试验总次数为：'，num2str(ntimes): msg2=['出现1-6的次数分别是：'，num2str(nlp1,nlp2,nIp3,n_lp4,n_lp5,nlp6]l: msg3=[各点出现的频率分别是：'，num2str(frequency]; disp(msg1)月 disp(msg2); disp(msg3); end

============================= matlab 模拟程序 ============================= function [ output_args ] = shaizi_sum( ntimes ) % 设置随机发生器，取得随机数 rng('default'); x=rand(1,ntimes); % 统计各点数出现的次数、频率 n_lp1=sum(x=1/6 & x=2/6 & x=3/6 & x=4/6 & x=5/6 & x<=6/6); frequency =[n_lp1,n_lp2,n_lp3,n_lp4,n_lp5,n_lp6]/ntimes; % 输出结果 msg1=['试验总次数为：',num2str(ntimes)]; msg2=['出现1~6的次数分别是：',num2str([n_lp1,n_lp2,n_lp3,n_lp4,n_lp5,n_lp6])]; msg3=['各点出现的频率分别是：',num2str(frequency)]; disp(msg1); disp(msg2); disp(msg3); end 例：计算机模拟抛掷骰子的试验 要求：输入实验次数，统计各点数(1~6点)出现的次数及频率

matlab模拟结果 >shaizi_sum(60) 试验总次数为：60 出现1-6的次数分别是：117971412 出现1点的频率是：0.183330.116670.150.116670.233330.2 >shaizi_sum(600) 试验总次数为：600 出现1-6的次数分别是：112100939511486 各点出现的频率分别是：0.186670.166670.1550.158330.190.14333 >>shaizi sum(6000) ≈0.166666 试验总次数为：6000 出现1~6的次数分别是：98198398710649701015 各点出现的频率分别是：0.16350.163830.16450.177330.161670.16917 >shaizi sum(60000) 试验总次数为：60000 出现1-6的次数分别是：10147100739906997799169981 各点出现的频率分别是：0.169120.167880.16510.166280.165270.16635 >>shaizi_sum(60000000) 试验总次数为：60000000 出现1-6的次数分别是：100025629999246999887910002461100001039996749 各点出现的频率分别是：0.166710.166650.166650.166710.166670.16661

============================= matlab 模拟结果 ============================= >> shaizi_sum(60) 试验总次数为：60 出现1-6的次数分别是：11 7 9 7 14 12 出现1点的频率是：0.18333 0.11667 0.15 0.11667 0.23333 0.2 >> shaizi_sum(600) 试验总次数为：600 出现1~6的次数分别是：112 100 93 95 114 86 各点出现的频率分别是：0.18667 0.16667 0.155 0.15833 0.19 0.14333 >> shaizi_sum(6000) 试验总次数为：6000 出现1~6的次数分别是：981 983 987 1064 970 1015 各点出现的频率分别是：0.1635 0.16383 0.1645 0.17733 0.16167 0.16917 >> shaizi_sum(60000) 试验总次数为：60000 出现1~6的次数分别是：10147 10073 9906 9977 9916 9981 各点出现的频率分别是：0.16912 0.16788 0.1651 0.16628 0.16527 0.16635 >> shaizi_sum(60000000) 试验总次数为：60000000 出现1~6的次数分别是：10002562 9999246 9998879 10002461 10000103 9996749 各点出现的频率分别是：0.16671 0.16665 0.16665 0.16671 0.16667 0.16661 1 0.166666 6 

说明：频率反映了在n次试验中，事件A发生的频繁程度： 频率越大，事件A在一次试验中发生的可能性就越大 用频率表征事件A发生的可能性大小的缺点： （1)频率具有波动性，使得频率难以确定； (2)需要通过大量的重复试验才能求得

说明：频率反映了在n 次试验中，事件A发生的频繁程度； 频率越大，事件A在一次试验中发生的可能性就越大. 用频率表征事件A发生的可能性大小的缺点： （1）频率具有波动性，使得频率难以确定； （2）需要通过大量的重复试验才能求得

1933年，苏联数学家柯尔莫哥洛夫提出了概率论的公理化 结构，给出了概率的严格定义，使概率论有了迅速的发展。 Andrey Nikolaevich Kolmogorov (1903-1987) 样本空间 频率的性质 概率

1933 年，苏联数学家柯尔莫哥洛夫提出了概率论的公理化 结构，给出了概率的严格定义，使概率论有了迅速的发展。 （1903 – 1987） Andrey Nikolaevich Kolmogorov 频率的性质 概率 样本空间

二、概率 1.定义（概率的公理化） 设E是随机试验，S是它的样本空间.对于E的每一事件 A赋于一个实数，记为P(A),称为事件A的概率，如果集合 函数P()满足下列条件： (1)非负性：对于每一个事件A,有P(A)≥0； (2)规范性：对于必然事件S,有P(S)=1; (③)可列可加性：设A,A,.是两两互不相容的事件， 即对于i≠j,AA,=0,i,j=1,2,.,则有 P(4 UA U.)=P(A)+P(A)+. 概率的可列可加性

. , ( ) , ( ) : A E S E A P A P  设 是随机试验， 是它的样本空间 对于 的每一事件 赋于一个实数 记为 称为事件 的概 如果集合 函数 满 率 足下列条件 ， (1) 非负性：对于每一个事件 A P A ，有 ( ) 0  ; (2) 规范性：对于必然事件 S P S , ( ) 1; 有 = 1 2 , , , , , 1, 2, (3) i j A A i j A A i j  =  = 可列可加 设 是两两互不相容的事件， 即 于 性： 对 ，则有 1 2 1 2 P A A P A P A ( ) ( ) ( ) = + + 概率的可列可加性 1. 定义(概率的公理化) 二、概率

2.性质(1)P(②)=0. (2) 若4A,A2,·,An是两两互不相容的事件，则有 有限可加性 P(4 UA,U.UA)=P(4)+P(4)+.+P(4,) (3)设A,B为两个事件，且ACB,则 P(B-A)=P(B)-P(A);P(B)2 P(A). 推广P(B-A)=P(BA)=P(B)-P(AB) 对于任意事件A,B成立。 (4)对于任一事件A,有P(A)≤1 (5)(逆事件的概率)对于任一事件A,有 P(A)=1-P(A) (6)(加法公式)对于任意两事件A,B有 重要公式！ P(AUB)=P(A)+P(B)-P(AB)

2. 性质 (1) ( ) 0. P  = 有限可加性 1 2 (2) , , , 若A A An是两两互不相容的事件，则有 1 2 1 2 ( ) ( ) ( ) ( ). P A A A P A P A P A n n = + + + (3) , , ( ) ( ) ( ) ( ) ( ). A B A B P B A P B P A P B P A  − = −  设 为两个事件，且 则 ； ( ) ( ) ( ) ( ) , P B A P B A P B P A B A B − = = − 对 于 任 意 事 件 成 立 。 推广 （4）对于任一事 件 A， 有 P A( ) 1  （5） (逆事件的概率) 对于任一事 件 A，有 P(A) = 1 − P(A) (6) ( ) , ( ) ( ) ( ) ( ). A B P A B P A P B P AB = + − 加法公式 对于任意两事件 有 重要公式！