《高等数学》课程教学资源（PPT课件）第九章多元函数微分法及其应用_9-6多元函数微分学的应用

第之节 第九章 多无菡数微分学的儿何应用 一、空间曲线的切线与法平面 二、曲面的切平面与法线 HIGH EDUCATION PRESS 上页下页返回结束

第六节 复习 目录 上页 下页 返回 结束 一、空间曲线的切线与法平面 二、曲面的切平面与法线 多元函数微分学的几何应用 第九章

复习：平面曲线的切线与法线 已知平面光滑曲线=f(x)在点(x01。)有 切线方程v-10=f'(o(x-Yo） 法线方程-'0= (-o f'(xo) 若平面光滑曲线方程为F(x,)=0.因 dr F(a.r) dr F(x） 故在点(0.0)有 切线方程 F(0,1o)(r-o)+F,(x00X-0)=0 法线方程 F(oox-xo)-F(xa16)(1-1%)=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

复习: 平面曲线的切线与法线 已知平面光滑曲线 切线方程 法线方程 若平面光滑曲线方程为 故在点 切线方程 法线方程 在点 有 有 因 机动 目录 上页 下页 返回 结束

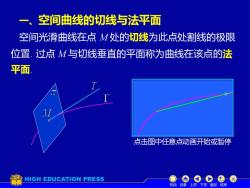
一、 空间曲线的切线与法平面 空间光滑曲线在点M处的切线为此点处割线的极限 位置.过点M与切线垂直的平面称为曲线在该点的法 平面 点击图中任意点动画开始或暂停 HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、空间曲线的切线与法平面 过点 M 与切线垂直的平面称为曲线在该点的法 机动 目录 上页 下页 返回 结束 位置. 空间光滑曲线在点 M 处的切线为此点处割线的极限 平面. 点击图中任意点动画开始或暂停

1.曲线方程为参数方程的情况 T:x=0().1=y(1).三=0(1) 设1=1n对应1(0.)》 1=7。+△1对应'(x6+△.10十A.0+A=） 割线M'的方程： Y-X0=y-0=2-0 △N 4 4 上述方程之分母同除以1.令△1→0.得 切线方程 O(t） /(o） o(1o） HIGH EDUCATION PRESS 机动目录上页下页返回结束

1. 曲线方程为参数方程的情况 切线方程 机动 目录 上页 下页 返回 结束

此处要求o(t6).'(o).0'(t不全为0， 如个别为0，则理解为分子为0 切线的方向向量： T=(ooyo.0'U月 称为曲线的切向量 T也是法平面的法向量，因此得法平面方程 0(1a(x-X0)+/(t0)1-'片0'(1a-二)=0 说明：若引进向量函数r(t)=((1).().0(t),则T 为T()的矢端曲线，而在1。处的导向量 Fuo)=(o'16)./'(a).0'U) 就是该点的切向量 等HIGH EDUCATION PRESS 机动目录上页下页返回结束

此处要求 也是法平面的法向量, 切线的方向向量: 称为曲线的切向量 . 如个别为0, 则理解为分子为 0 . 机动 目录 上页 下页 返回 结束 不全为0, 因此得法平面方程 说明: 若引进向量函数 , 则  为 r (t) 的矢端曲线, 处的导向量 就是该点的切向量

例1.求圆柱螺旋线x=Rcoso.Y=Rsin0.:=o在 ®=号对应点处的切线方程和法平面方程 解：由于x'=-Rsin0,'=Rc0so.:'=k.当p=号时. 对应的切向量为T=(-R.0.k),故 十=-R-ξk Io(0.R.号k) 切线方程 R 0 即 kr+R=-琴Rk=0 r-R=0 法平面方程-RX+(二-ξk)=0 即 Rx-k:+ξk=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1. 求圆柱螺旋线 对应点处的切线方程和法平面方程. 切线方程 法平面方程 即 即 解: 由于 对应的切向量为 在 机动 目录 上页 下页 返回 结束 , 故

2.曲线为一般式的情况 光滑曲线T: F(x.1.2)=0 G(x.1.2)=0 当= C(F.G) 7: ≠0时，「可表示为 0(x) 且有 0(.2) 二=/(x) dr 1(F.G) d=1(F.G) dx Je(5.x)' dr J(.y) 曲线上一点M(x1,二)处的切向量为 T={1.o'(xo)./'(ra月 12(F.G) 1(F.G) (.r) (X1) HIGH EDUCATION PRESS 机动目录上页下页返回结束

2. 曲线为一般式的情况 光滑曲线 当 曲线上一点 时,  可表示为 , 且有 处的切向量为 机动 目录 上页 下页 返回 结束

或7= C(F.G) (F.G) C(F.G) (1a) c(三.) C(x.） M 则在点M(xa.1o.o有 切线方程 r-0 '-1'0 -0 C(F.G) Q(F.G) (F.G) .=) M e(s."a e(x.T) Q(F.G) 法平面方程 Q(F.G) 0(1.三) (x-N0)+ C(Ξ.r (-To) Q(F.G) (三- Ξ0）=0 (x.)M HIGH EDUCATION PRESS 机动目录上页下页返回结束

则在点 切线方程 法平面方程 有 或 机动 目录 上页 下页 返回 结束

法平面方程 Q(F.G) C(F.G) (1.3) es.w M-% Q(F.G) Cx.1） ,M-6)-0 也可表为 Y-3X0 1-1'0÷-=0 F(MD)F(M)F(M) =0 Gx(M)G(M)G:(M) HIGH EDUCATION PRESS 机动目录上页下页返回结束

也可表为 法平面方程 机动 目录 上页 下页 返回 结束

例2.求曲线x2+2+2=6.r+1y+:=0在点 M(1,-2,1)处的切线方程与法平面方程 解法1令F=2+2+:2.G=+y+.则 (F.G22 6(.)y11y =2(1-） =-6: (F.G) =0: (F.G) =6 e(.x) / e(x.y)a 切向量 7=(-6.0.6) -1=y+2=- x+2-2=0 切线方程 即 -6 6 1+2=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例2. 求曲线 在点 M ( 1,–2, 1) 处的切线方程与法平面方程. 切线方程 解法1 令 则 即 切向量 机动 目录 上页 下页 返回 结束