《高等数学》课程教学资源（课件讲稿）第九章_9.4多元复合函数的求导法则

第四节多元复合晶数的 求导法则 ·一、链式法则 ·二、金微分形式的不变性 ·三、小结思考题

第四节 多元复合函数的 求导法则 • 一、链式法则 • 二、全微分形式的不变性 • 三、小结 思考题

一、链式法则 1、一元函数与多元函数复合的情形 (z=f(u,),u=p(t),y=w(t)的情形) 定理1如果函数u=p(t)及y=y(t)在点t可导，函数 z=f(u,v)在对应点(u,v)具有连续的偏导数，则复 合函数z=f(p(t),业(t)在对应点处可导，且导数 可表示为 dz az du oz dv dt Ou dt t Ov dt 证设t获得增量△t 则△u=p(t+△t)-p(t),△v=V(t+△)-y(t)；

证 则     u t t t   ( ) ( ),      v t t t   ( ) ( ); 设 t t 获得增量  ， 1、一元函数与多元函数复合的情形 ( ) ( ) , ( , ) ( , ) ( ( ), ( )) 1 u t v t t z f u v u v z f t t t dz z du z dv dt u dt v dt               如果函数 及 在点 可导 函数 在对应点 具有连续的偏导数，则复 合函数 在对应点 处可导，且导数 可表示为 定理 一、链式法则 z u v t ( ( , ), ( ), ( ) ) z f u v u t v t      的情形

由于函数z=f(w,v)在(w,)点具有连续的偏导数 4s9 AAv+AAv, Ou 当△u→0，△y→0时，E-→0,62→0 △zOz△u,Oz△y,。△u,。△y △tOu△t'Ov△t +61t +82 At 当△t→0时，u→0，△y→0 y血，A如 △W dv △t'dt At dt d lim △z_ozdu,zdy dt △t-→0△t Ou dt dt

1 2 , z z z u v u v u v                1 2 z z u z v u v t u t v t t t                       , , u du v dv t dt t dt       由于函数z f u v u v  ( , ) ( , ) 在 点具有连续的偏导数 当      t u v 0 0 0 时， ， 1 2 当      u v 0 0 0 0 ， 时，  ， 0 lim . t dz z z du z dv dt t u dt v dt             

上定理的结论可推广到中间变量多于两个的情况. 例如z=f(w,y,w),u=p(),v=y(t),w=o(t) dz az du oz dy az dw dt Ou dt'Ov dt'Ow dt 以上公式中的导数 名称为金都款

上定理的结论可推广到中间变量多于两个的情况. dz z du z dv z dw dt u dt v dt w dt          u v w z t 以上公式中的导数 称为全导数. dz dt 例如z f u v w u t v t w t     ( , , ) , ( ), ( ), ( )   

设z=w+sim6而u=e,v=cos6求全导数 dz az du oz dv az 解 dt Ou dt'Oy dt'Ot ve'-usint+cost e'cost-e'sint+cost e'(cost-sint)+cost

解 dz z du z dv z dt u dt v dt t            ve u t t t   sin  cos e t e t t t t  cos  sin  cos e (cost sin t) cost. t    1 sin cos . t dz z uv t u e v t dt 例 设     ，而 ， ，求全导数

说明：若定理中f(u,)在点(u,v)偏导数连续 减弱为偏导数存在，则定理结论不一定成立 u'v 例如：=fu,)={w+,4+心≠0 u=t,v=t 0, 2+v2=0 Oz 易知：∂u . =f(0,0)=0,0z 0,0(0,0)=0 但复合函数乙=f(t,t)= t 2 dz 1 Oz du oz dy dt 2 Ou dt oy dt =01+01=0

说明: 若定理中 例如: 2 2 2 2 2 2 2 , 0 ( , ) 0, 0 u v u v z f u v u v u v             u t v t   , 易知: 但复合函数 ( , ) 2 t z f t t   d 1 d 2 z t   d d 0 1 0 1 0 d d z u z v u t v t             偏导数连续 减弱为偏导数存在，则定理结论不一定成立

2、多元函数与多元函数复合的情形 (z=f(u,v),u=p(x,y),y=y(x,y)的情形) 定理2如果函数u=p(x,y)及v=y(x,y)在点(x,y) 具有对x及对的偏导数，函数z=f(,)在对应点 (山，)具有连续偏导数，则复合函数z=fIp(x,y), (x,y)川在点(x,y)的两个偏导数都存在，且有 Oz Oz Ou Oz Ov Bx ou ax Oy ox Oz Oz ou 8y ou ay ov dy

2、多元函数与多元函数复合的情形 ( , ) ( , ) ( , ) ( , ) ( , ) [ ( , ), ( , )] ( , ) , . 2 u x y v x y x y x y z f u v u v z f x y x y x y z z u z v x u x v x z z u z v y u y v y                                 如果函数 及 在点 具有对 及对 的偏导数，函数 在对应点 具有连续偏导数，则复合函数 在点 的两个偏导数都存在，且有 定理 ( ( , ), ( , ), ( , ) ) z f u v u x y v x y      的情形

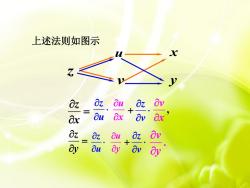
上述法则如图示 Ou 加加创

u v x z y 上述法则如图示 z x    z u    u x   z v     , v x   z y    z u    u y   z v     . v y  

类似地再推广，设u=p(x,y八v=(x,y)及w=w(x,) 在点(x,y)具有对x及对的偏导数，函数z=f(,y,w) 在对应点(，w)具有连续偏导数，则复合函数 z=fp(x,y),(x,y),w(x,y)川在点(x,y)的两个偏导数 都存在，且有 Oz Oz ou oz Ov Oz ow 一十 一+ Ox Ou ax Oy OxOw ax Oz Oz ou Ov Ow ay ou ay ov ay Ow Oy

z w v u y x , ( , ) ( , ) ( , ) ( , ) ( , , ) ( , , ) [ ( , ), ( , ), ( , )] ( , ) , u x y v x y w w x y x y x y z f u v w u v w z f x y x y w x y x y z z u z v z w x u x v x w x z z u y u y                                  类似地再推广 设 、 及 在点 具有对 及对 的偏导数，函数 在对应点 具有连续偏导数，则复合函数 在点 的两个偏导数 都存在，且有 . z v z w v y w y          

例2设z=e“siny,而u=Xy,v=x+y, 求及 O 解 ooou Bov=e"sinv.y+e"cosv-I ax Ou ax av ax =e[ysin(x+y)+cos(x+y)], ouv=e"simv.xe"cosv-I ay ou ay av ay =e[xsin(x+y)+cos(x+y)]

解 z z u z v x u x v x               sin cos 1 u u     e v y e v [ sin( ) cos( )], xy     e y x y x y z z u z v y u y v y               sin cos 1 u u     e v x e v [ sin( ) cos( )]. xy     e x x y x y 2 sin . u z e v u xy v x y z z x y         例 设 ，而 ， ， 求 及