《高等数学》课程教学资源（课件讲稿）第十章_10-2二重积分的计算

第二节二重积分的计算 ·一、利用直角坐标计算二重积分 ·二、利用极坐标计算二重积分 ·三、小猪徐习毁

第二节 二重积分的计算 • 一、利用直角坐标计算二重积分 • 二、利用极坐标计算二重积分 • 三、小结 练习题

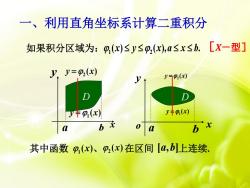
一、利用直角坐标系计算二重积分 如果积分区域为：p,(x)≤y≤p,(x),a≤r≤b.[X-型] yy=0(x) y59(x) y丰9x) y+9() b b七 其中函数p,(x)、p(x)在区间[4，b上连续

如果积分区域为： 1 2   ( ) ( ), . x y x a x b     其中函数 、 在区间 上连续. 1  ( ) x 2  ( ) x [ , ] a b ［X－型］ 一、利用直角坐标系计算二重积分 1 y x   ( ) 2 y x   ( ) x o b y D a 1 y x   ( ) 2 y x   ( ) x b o y D a

∬fc,)do的值等于以D为底，以曲面 z=f(化，y)为曲顶柱体的体积. z=f(x,y) 应用计算“平行截 面面积为已知的立 体求体积”的方法， A(x) 三9() 得=

( , ) ( , ) D f x y d D z f x y    的 值等 于 以 为底，以 曲 面 为 曲 顶柱体 的 体积． 应用计算“平行截 面面积为已知的立 体求体积”的方法 , 2 1 ( ) ( ) ( ) ( , ) xx A x f x y dy    得 z f x y  ( , ) x y zO D 2 y x   ( ) a x b A (x ) 1 y x   ( )

于是y=JAe=fx, 则jfc)aa干f,依. 二次积分 习惯上二次积分也写作 amfc,a

二次积分 2 1 ( ) ( ) ( ) [ ( , ) ] . b b x a a x V A x dx f x y dy dx     于是   2 1 ( ) ( ) ( , ) [ ( , ) ] . b x a x D f x y d f x y dy dx     则   2 1 ( ) ( ) ( , ) b x a x dx f x y dy    习惯上二次积分也写作

如果积分区域为：)≤x≤y以，c≤y≤d. [Y-型] d x=V2(0y) x=2y) d x=v(y) D x=(y) c xa=Jxaw fca

如果积分区域为： ［Y－型］ 2 1 2 1 ( ) ( ) ( ) ( ) ( , ) [ ( , ) ] = ( , ) d y c y D d y c y f x y d f x y dx dy dy f x y dx            1 2   ( ) ( ), . y x y c y d     x d o y c 1 x y  ( ) 2 x y  ( ) D y 1 x y  ( ) 2 x y  ( ) x d o c

说明：(1)若积分区域既是X-型区域又是Y-型区域， 则有nfc,)dxdy y=92(x) (xydy t=wy) =920y) =afxax b 为计算方便，可选择积分序，必要时还可以交换积分序 (2)若积分域较复杂，可将它分成 若干X型域或Y型域，则 =+川+

o x y 说明: (1) 若积分区域既是X–型区域又是Y –型区域 , ( , )d d D f x y x y  为计算方便,可选择积分序, 必要时还可以交换积分序. 2 y x   ( ) o x y D a b 1 x y  ( ) 2 x y  ( ) d c 则有 1 y x   ( ) 2 1 ( ) ( ) d ( , )d b x a x x f x y y      2 1 ( ) ( ) d ( , )d d y c y y f x y x      (2) 若积分域较复杂,可将它分成 若干X-型域或Y-型域 ,则 D1 D2 D3 D D D D 1 2 3       

利用直系计算二重积分的步骤 (1)画出积分区域的图形，求出边界曲线交点坐标； (2)根据积分域类型，确定积分次序； (3)确定积分限，化为二次定积分； (4)计算两次定积分，即可得出结果 注意：二重积分转化为二次定积分时，关键在 于正确确定积分限，一定要做到熟练、准确

注意：二重积分转化为二次定积分时，关键在 于正确确定积分限,一定要做到熟练、准确。 利用直系计算二重积分的步骤 （1）画出积分区域的图形,求出边界曲线交点坐标； （3）确定积分限，化为二次定积分； （2）根据积分域类型, 确定积分次序； （4）计算两次定积分，即可得出结果

例1.计算I=儿。ydo,其中D是直线y=1,x=2,及 y=x所围的闭区域。 解法1.将D看作X-型区域，则D: 1≤y≤x 1≤x≤2 Idxfxyax 2 y=x 金细8期■发g年年年装自 i片r-]ar 解法2.将D看作y-型区域则D:sx≤2 -可a时w=i-3小-8

x y 2 1 1 y x  o 2   2 2 1 1 2 d 2 x y y y   例1. 计算 d , D I x y    其中D 是直线 y＝1, x＝2, 及 y＝x 所围的闭区域. x 解法1. 将D看作X–型区域, 则 1 : 1 2 y x D x        2 1 1 d d x I x x y y      2 2 1 1 d 2 1 x  x y x    2 3 1 1 1 d 2 2   x x x  9 8  解法2. 将D看作Y–型区域, 则 2 : 1 2 y x D y        2 2 1 d d y I y x y x    2 3 1 1 2 d 2 y y y          9 8  y

例2.计算川xydo,其中D是抛物线广=x及直线 y=x-2所围成的闭区域。 解：为计算简便，先对x后对y积分，y =X 则1 4 -1≤y≤2 -1 y=x-2 Jydc =y=0+2- -日誓

例2. 计算 d , D x y   其中D 是抛物线 所围成的闭区域. 解: 为计算简便, 先对 x 后对 y 积分, 2 2 : 1 2 y x y D y          d D  x y   2 2 2 1 d y y y xydx      2 2 2 2 1 1 d 2 y y x y y           2 2 5 1 1 [ ( 2) ] d 2 y y y y      D 2 y x  y x   2 2 1 4 o y x y 及直线 则

例3.计算 川d、其中D是直线)- 所围成的闭区域。 解：由被积函数可知，先对x积分不行， y=x X=元 因此取D为X-型域： 0≤y≤x 元 D: 0≤x≤π 灯ndd=nad =∫sinxdx=-cosx]W=2 说明：有些二次积分为了积分方便，还需注意积分顺序

例3. 计算 sin d d , D x x y x  其中D 是直线 所围成的闭区域. o x y D  x   解 y x  : 由被积函数可知, 因此取D 为X – 型域 : 0 : 0 y x D x         sin d d D x x y x   0 sin dx x     2 0 0 sin d d x x x y x     先对 x 积分不行, 说明: 有些二次积分为了积分方便, 还需注意积分顺序