《高等数学》课程教学资源（课件讲稿）第十一章_11.4对面积的曲面积分

第四节对面积的曲面积分 ·一、桡念的引入 ·二、对面积的曲面积分的定义 ·三、计算法 ·四、小结思考题

第四节 对面积的曲面积分 • 一、概念的引入 • 二、对面积的曲面积分的定义 • 三、计算法 • 四、小结 思考题

一、概念的引入 实例 若曲面Σ是光滑的，它的面密度为连 续函数p(x,y,z),求它的质量. 所谓曲面光滑即 000 曲面上各点处都有 4000 切平面，且当点在曲 面上连续移动时，切 2000 平面也连续转动. -40-200 20 40

一、概念的引入 若曲面是光滑的, 它的面密度为连 续函数( x, y,z), 求它的质量. 实例 所谓曲面光滑即 曲面上各点处都有 切平面,且当点在曲 面上连续移动时,切 平面也连续转动

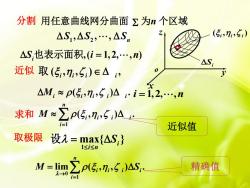
分割用任意曲线网分曲面Σ为n个区域 △S1,△S2,.,△Sn (5,17,5) △S,也表示面积，(i=1,2,.,n) △S 近似取(5,7,5)∈△i) △M1≈p(5,n,5)A-i=1,2,n 求和M≈∑p(5,n,5,)A 近似值 取极限设2=max{△S;} 1<i<n M=m2p5,m6,)△. 精确值

分割 i n  1,2, , ,( 1,2, , )   S i n i也表示面积 1 2 , , ,    S S Sn 用任意曲线网分曲面  为n 个区域 近似 1 ( , , ) . n i i i i i M     S     近似值 ( , , ) , 取    i i i i  S ( , , ) .    Mi i i i i     S 取极限 0 1 lim ( , , ) . n i i i i i M S           精确值 1 max{ }i i n  S   设   Si  ( , , ) i i i    y z o x 求和

二、对面积的曲面积分的定义 定义设曲面Σ是光滑的，函数f(x,y,)在∑ 上有界，把∑分成n小块△S:(△S;同时也表示 第i小块曲面的面积)，设点(5,7,5)为△S:上任 意取定的点，作乘积f(5,n,5)△S, 并作和∑f(5,7,5)·△S,如果当各小块曲面 i=1 的直径的最大值入→0时，这和式的极限存在， 则称此极限为函数f(x,y,z)在曲面∑上对面积 的曲面积分或第一类曲面积分

二、对面积的曲面积分的定义 设曲面是光滑的, 函 数 f (x, y,z)在 上有界, 把分 成n小 块Si（Si同时也表示 第i小块曲面的面积）,设点( , , )  i i  i 为Si上任 意取定的点,作乘积 ( , , ) i i i f    Si , 并作和  n i i i i f 1 ( , , ) Si , 如果当各小块曲面 的直径的最大值  0时, 这和式的极限存在, 则称此极限为函数 f ( x, y,z)在曲面上对面积 的曲面积分或第一类曲面积分. 定义

记为 J∬fx,z)aS. 即J∬f(x,z)S=1im∑f5,n,5)As: 入→0 i=1 其中f(x,y,z)叫被积函数，叫积分曲面. 当f(x,y,z)在光滑曲线曲面Σ上连续时， 对曲面的曲面积分丁f(x,少，z)S存在 若Σ可分为分片光滑的曲面Σ，及Σ2，则 f2s=/,s+∬s

即   f (x, y,z)dS i i i n i   f i S   lim ( , , ) 1 0     记为   f ( x, y,z)dS.   f (x, y,z)dS       1 2 f (x, y,z)dS f ( x, y,z)dS. 1 2 若   可分为分片光滑的曲面 及 , 则 其中 f x y z ( , , ) . 叫被积函数，叫积分曲面 ( , , ) , ( , , ) . f x y z f x y z dS    当 在光滑曲线曲面 上连续时 对曲面的曲面积分 存在

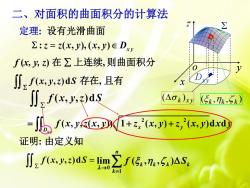
二、对面积的曲面积分的计算法 定理：设有光滑曲面 ∑：z=z(x,y),(x,y)eDxy f化，乃)在∑上连续，则曲面积分 小2fx,八，zds存在，且有 ∬2fc,yds (AOk)xy (5k,7k,5k】 ++:dxdy 证明：由定义知 ∬2fc,a)dS=lim∑f(5,n,5)△S。 2→0 k=

o x y z 定理: 设有光滑曲面 f (x, y, z) 在  上连续, f x y z S ( , , )d 存在, 且有   2 2 ( , , ( , )) 1 ( , ) ( , )d d x y x y D    f x y z x y z x y z x y x y  二、对面积的曲面积分的计算法 则曲面积分 证明: 由定义知 0 1 lim ( , , ) n k k k k k f S         Dxy ( , , )  k k  k k x y ( ) 

而AS.=∬aa,V1+z(x)+z,(,月ddy =√1+z2(5,)+z,2(5,)(△o)x .j∬fx,yz)dS =∑f5na,z5,7》 V1+z2(5,)+z,2(5,)(△o)x =1im∑f(5,n,3(5,7s》 (②光滑) 2-→0 k=1 √1+zx2(5,n)+乙，2(5,7)（△o)xy =。f(c,zx,y√1+z2(c,y)+z,2c,)dxdy

2 2 1 ( , ) ( , ) ( ) x k k y k k k x y     z z          2 2 1 ( , ) ( , ) ( ) x k k y k k k x y    z z          2 2 1 ( , ) ( , ) ( ) x k k y k k k x y    z z      2 2 ( , , ( , )) 1 ( , ) ( , )d d x y x y D    f x y z x y z x y z x y x y f x y z S ( , , )d    而 ( 光滑 )

其他情况 1. 若曲面Σ：y=y(x,) 则∬f(x,y,z)S flx,y(x,z),l+y2+y"dxdzs Dx 2.若曲面2：x=x(0y,z) 则 ∬f(x,y,z)ds =J∬fx(0,z少，2小V1+X2+x

[ , ( , ), ] 1 ; 2 2 f x y x z z y y dxdz Dxz  x z        则 f (x, y,z)dS [ ( , ), , ] 1 . 2 2 f x y z y z x x dydz Dyz  y z        f (x, y,z)dS 2. ( , ) 若曲面  ： x x y z 则 1. : ( , ) 若曲面 y y x z 其他情况

例1，计算面积分小儿，其中工是球面+少+女 =a被平面z=h(0<h<a)截出的顶部. 解：∑：z=Va2-x2-y2,(c,)eDy Dyx2+y2≤a2-h2 +2+区-后-少 -aa=a1,2 =o-pm]=2xah月

Dxy 例1. 计算曲面积分 其中是球面 被平面 截出的顶部. 解: 2 2 2 2 : D x y a h x y    2 2 2 2 2 1 x y a z z a x y      d S z   2 2 2 2 2 0 0 d d a h a a           2 2 1 2 2 2 ln( ) 2 0 a h   a a           2 2 2 d d Dx y a x y a x y     o x z y  h a

补充 设分片光滑的曲面关于yOz面对称，则 ∬fx,ds 0, 当f(x,z)为x的奇函数 =2fx,%s.当fx,为x的偶函数 其中∑1：x=x(y,2)≥0

补充 设分片光滑的 f x y z S ( , , )d   x的奇函数 x的偶函数 1 2 ( , , )d . f x y z S   1 其中    : ( , ) 0. x x y z     0, 曲面Σ关于yOz面对称, 则 当f x y z ( , , )为 当f x y z ( , , )为