《高等数学》课程教学资源（课件讲稿）第八章_8.4空间直线及其方程

第四节空间直孩及其方程 ·一、空间直孩的一般方程 ·二、空间直孩的对称式方程与参教方程 ·三、两直孩的夹角 ·四、直孩与平面的夹角 ·五、年面束 ·六、小结

第四节 空间直线及其方程 • 一、空间直线的一般方程 • 二、空间直线的对称式方程与参数方程 • 三、两直线的夹角 • 四、直线与平面的夹角 • 五、平面束 • 六、小结

一、 空间直线的一般方程 定义空间直线可看成两平面的交线. Π1：Ax+By+C1z+D1=0 Π2：A2x+B2Jy+C2+D2=0 Ax+By+C+D=0 A2x+B2y+C27+D2=0 空间直线的一般方程x

x y z o 1 2 定义 空间直线可看成两平面的交线． : 0 1 A1 x  B1 y  C1z  D1  : 0 2 A2 x  B2 y  C2 z  D2             0 0 2 2 2 2 1 1 1 1 A x B y C z D A x B y C z D 空间直线的一般方程 L 一、空间直线的一般方程

二、空间直线的对称式方程与参数方程 方向向量的定义： 如果一非零向量平行于一 条已知直线，这个向量称为 这条直线的方向向量. 5={m,n,ph,Mo(xo,5o,zo), VM∈L,M(x,y,z), MoMI∥ MoM={x-xo,y-yo,-Z03

x y z o 方向向量的定义： 如果一非零向量平行于一 条已知直线，这个向量称为 这条直线的方向向量． s  L ( , , ), 0 0 0 0 M x y z M0   M  M  L, M ( x, y,z), M M s  0 // s  {m, n, p},  { , , } 0 0 0 0 M M  x  x y  y z  z 二、空间直线的对称式方程与参数方程

x-xoy-yo3-Z0 直线的对称式方程 n 令七-0=y-4=-0=t m. n. x=x+mt 直线的一组方向数 y=yo+nt 方向向量的余弦称为 Zo pt 直线的方向余弦， 直线的参数方程

p z z n y y m x x0 0  0     直线的对称式方程 t p z z n y y m x x      令  0 0 0            z z pt y y nt x x mt 0 0 0 直线的一组方向数 方向向量的余弦称为 直线的方向余弦. 直线的参数方程

例1用对称式方程及参数方程表示直线 x+y+z+1=0 2x-y+3z+4=0 解 在直线上任取一点(K,y,0) 取七，=1→+名，+2=0 y-3z0-6=0 解得y=0,z=-2 点坐标(1,0，-2)

例1 用对称式方程及参数方程表示直线 1 0 2 3 4 0 x y z x y z            解 在直线上任取一点 ( , , ) 0 0 0 x y z 取 1 x0  , 3 6 0 2 0 0 0 0 0           y z y z 解得 0, 2 y0  z0   点坐标 (1,0, 2)

因所求直线与两平面的法向量都垂直 取5=元1×i2= 111 ={4,-1,-3}, 2-13 对称式方程 x-1=y-0 z+2 4 -1-3 x=1+4t 参数方程y=-t z=-2-3t 还有其他方法吗

因所求直线与两平面的法向量都垂直 取 n1 n2 s       {4, 1, 3}, 对称式方程 , 3 2 1 0 4 1       x  y z 参数方程 . 2 3 1 4             z t y t x t 1 1 1 2 1 3 i j k   还有其他方法吗

法二 x++1=0 (1) 2x①七3z+4=0 (2) (1)+(2)可消去. → 38+4z+5=0 3(1)-(2)可消去z →区+4y-1=0 两个方程中，每一个只有两个变量，解出 共同的变量x.写成比例式，即得对称式方程 1 5 4 x= 1 4

写成比例式, 1 5 4 4 1 3 4 4 y z x       法二 1 0 2 3 4 0 x y z x y z            (1) (2) 3 4 5 0 x z    3(1) (2) .  可消去z x y    4 1 0 (1) (2) .  可消去y 两个方程中, 每一个只有两个变量,   共同的变量 即得对称式方程. 解出 x

注.直线的一般方程化为对称式方程（重要） 怎样将直线的一般方程化为对称式方程 有两种方法 ()在直线上找一定点，再求出方向向量， 即写出对称式方程. (2)用代数的消元法化为比例式；

注. 直线的一般方程化为对称式方程 怎样将直线的一般方程 (2) 用代数的消元法化为比例式; 有两种方法 (1) 在直线上找一定点,再求出方向向量, 即写出对称式方程. (重要) 化为对称式方程

例2一直线过点4(2，-3,4)，且与y轴垂直相交， 求其方程。 解 因为直线和y轴垂直相交， 所以交点为B(0,-3,0), 取5=BA={2,0,4, 所求直线方程，2=y+3_名-4 2 0 4

解 因为直线和 y 轴垂直相交, 所以交点为 B(0, 3, 0), 取 s  BA   {2, 0, 4}, 所求直线方程 . 4 4 0 3 2 2     x  y z 2 (2, 3,4) . 例 一直线过点A y  ，且与 轴垂直相交， 求其方程

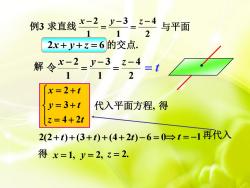
例3求直线七-2 =y-33-4 与平面 1 2 2x+y+z=6的交点. 解令七-2 _y-3z-4 2 =t x=2+t y=3+t 代入平面方程，得 z=4+2t 2(2+)+(3+)+(4+2t)-6=0曰t=-1再代入 得x=1,y=2,=2

2 4 1 3 1 2     x  y z 令 2 4 1 3 1 2     x  y z 得 2x  y  z  6 解            z t y t x t 4 2 3 2 2(2 t) (3 t) (4 2t) 6  0 t  1 再代入 代入平面方程, 例3 求直线 与平面 的交点.  t  得 x  1, y  2, z  2