《高等数学》课程教学资源（课件讲稿）第十一章_11.7 斯托克斯公式 环流量与旋度

第七节斯托克斯公式环流量与旋度 ·一、斯花克斯公式 ·二、简单应用 ·三、物理意义一环流量与旋度 ·四、小结 思考题

第七节 斯托克斯公式 环流量与旋度 • 一、斯托克斯公式 • 二、简单应用 • 三、物理意义—环流量与旋度 • 四、小结 思考题

一、斯托克斯(stokes)公式 定理1设厂为分段光滑的空间有向闭曲线，Σ是 以T为边界的分片光滑的有向曲面，Γ的正向与 Σ的侧符合右手规则，函数P(x,y,z),2(x,y,z), R(x,y,z)在包含曲面2在内的一个空间区域内具 有一阶连续的偏导数，则有公式 器+ axkc+( =∮Pk+Q+Rd 斯托克斯公式

一、斯托克斯(stokes)公式 斯托克斯公式 ( , , ), ( , , ), ( , , ) ( ) ( 1 ) ( ) P x y z Q x y z R x y z R Q P R Q P dydz dzdx dxdy y z z x x y Pdx Qdy Rdz                               设 为分段光滑的空间有向闭曲线， 是 以 为边界的分片光滑的有向曲面， 的正向与 的侧符合右手规则，函数 在包含曲面 在内的一个空间区域内具 有一阶连续的偏导数，则有公式 定理

便于记忆形式 dydz dzdx dxdy 0 0 ay Ox =∮nP+O+Rk P 2 R 另一种形式 cosa cos B cosy 0 0 Ox ay Ox S=∮Pc+O+Rdk P Q R 其中i={cosa,cosB,c0sy}

dydz dzdx dxdy Pdx Qdy Rdz x y z P Q R              cos cos cos dS Pdx Qdy Rdz x y z P Q R                 另一种形式 n  {cos,cos  ,cos }  其中 便于记忆形式

Stokes公式的实质： 表达了有向曲面上的曲面积分与其边界曲线 上的曲线积分之间的关系. (当Σ是xoy面的平面闭区域时) 斯托克斯公式 特殊情形 格林公式

Stokes公式的实质: 表达了有向曲面上的曲面积分与其边界曲线 上的曲线积分之间的关系. 斯托克斯公式 特殊情形 格林公式 (当Σ 是xoy面的平面闭区域时)

二、简单的应用 例1计算曲线积分∮z+x+y,其中T 是平面x+y+z=1被三坐标面所截成的三角 形的整个边界，它的正向与三角形上侧的法 向量之间符合右手规则. 解按斯托克斯公式，有 手zd+x+ydk =j小yd+dkdc+dcdy

二、简单的应用 解 按斯托克斯公式, 有 zdx xdy ydz       dydz  dzdx  dxdy Dxy x y z n 1 1 1 0 1 1 zdx xdy ydz x y z        例 计算曲线积分 ，其中 是平面 被三坐标面所截成的三角 形的整个边界，它的正向与三角形上侧的法 向量之间符合右手规则

由于Σ的法向量的三个方向余弦都为正， 再由对称性知： ∬dk+dkdc+=3∬do D,如图 重+x+啦=3

  dydz  dzdx  dxdy    Dxy 3 d x y o 1 1 Dxy 2 3  由于的法向量的三个方向余 弦都为正， 再由对称性知： Dxy如图 zdx xdy ydz    

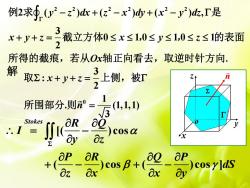
例2求∮y2-z)+(2-x2)+(x2-2),r是 +y+z三截立方体0≤x≤，0≤≤0≤z≤1的表面 所得的载截痕，若从Ox轴正向看去，取逆时针方向. 取z+一上侧，r 解 1 所围部分.则= (1,1,1) Stokes .I= )cosa Ox + 2_a那)cosrldS

解 z x y o  n   [( )cos ( )cos ( )cos ] Stokes R Q I y z P R Q P dS z x x y                        2 2 2 2 2 2 2 ( ) ( ) ( ) , 3 0 1 0 1 0 1 2 y z dx z x dy x y dz x y z x y z Ox                 例 求 是 截立方体 ， ， 的表面 所得的截痕，若从 轴正向看去，取逆时针方向. 0 3 : 2 1 . (1,1,1) 3 x y z n       取 上侧，被 所围部分 则

1= -)csa+(P-9 ，Oz R)cosB 3∬x+y+zs 2:x+y+z= 0.5 =-255a=号 .20.40.60.811.2

[( )cos ( )cos ( )cos ] R Q P R I y z z x Q P dS x y                         z x y o  n   Dxy 2 3 x  y  2 1 x  y  4 ( ) 3 x y z dS       3 2 4 3 3 2 x y z dS          ： 9 2 3 3 . 2 Dxy     dxdy 

三、物理意义-环流量与旋度 1.环流量的定义： 设向量场 A(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k 则沿场A中某一封闭的有向曲线C上的曲线积分 T=∮。A.否=∮Pc+2+Rk 称为向量场A沿曲线C按所取方向的环流量

三、物理意义-环流量与旋度 ( , , ) ( , , ) ( , , ) ( , , ) . C C A x y z P x y z i Q x y z j R x y z k A C A ds Pdx Qdy Rdz A C            设向量场 则沿场 中某一封闭的有向曲线 上的曲线积分 称为向量场 沿曲线 按所取方向的环流量 1. 环流量的定义:

利用stokes公式，有 i j 环流量「=∮A5=川 品 ka沈R d P Q 2.旋度的定义： j E 称向量 品 a小 为向量场的旋度(rot小. Bx P 2 R

C i j k A ds dS x y z P Q R             环流量   利用stokes公式, 有 2. 旋度的定义: ( ) . i j k x y z P Q R rotA       称向量 为向量场的旋度