《高等数学》课程教学资源（课件讲稿）第十一章_11.5对坐标的曲面积分

第五节对坐标的曲面积分 ● 一、有向曲面及曲面元素的投影 ·二、橇念及性质 ·三、计算法 四、禹美曲面积分之同的联素 ·五、小结思考题

第五节 对坐标的曲面积分 • 一、有向曲面及曲面元素的投影 • 二、概念及性质 • 三、计算法 • 四、两类曲面积分之间的联系 • 五、小结 思考题

一、有向曲面及曲面元素的投影 双侧曲面 ·曲面分类 曲面分内侧 单侧曲面 和外侧 曲面分上侧 曲面分左侧 和下侧 和右侧 莫比鸟斯带 (单侧曲面的典型)

一、有向曲面及曲面元素的投影 • 曲面分类 双侧曲面 单侧曲面 莫比乌斯带 曲面分上侧 和下侧 曲面分内侧 和外侧 曲面分左侧 和右侧 (单侧曲面的典型)

曲面法向量的指向决定曲面的侧. 决定了侧的曲面称为有向曲面. 曲面的投影问题：在曲面Σ上取一小块曲面△S, 曲面△S在xOy面上的投影（△S),为 (Ao),当c0sy>0时 当cosy<0时. 0 当cosy=0时 其中（△o)表示投影区域的面积， 类似可规定 y是曲面的法向量与z轴的夹角. (AS)(AS)

曲面法向量的指向决定曲面的侧. 决定了侧的曲面称为有向曲面. 曲面的投影问题: ( ) 曲面  S xoy S 在 面上的投影 xy为 ( ) cos 0 ( ) ( ) cos 0 . 0 cos 0 xy S xy xy                   当 时 当 时 当 时 ( ) . xy z   其中  表示投影区域的面积， 是曲面的法向量与 轴的夹角 在曲面  上取一小块曲面 S， 类似可规定 ( ) , ( )   S S yz zx

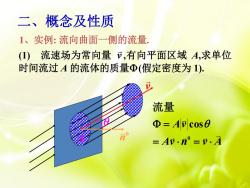
二、概念及性质 1、实例：流向曲面一侧的流量。 (1)流速场为常向量)，有向平面区域A,求单位 时间流过A的流体的质量Φ（假定密度为1）. 流量 Φ=Ac0s0 =Av.n=v.A

1、实例: 流向曲面一侧的流量. (1) 流速场为常向量 v  ,有向平面区域 A,求单位 时间流过 A 的流体的质量(假定密度为 1). A v  0 n   A Av n v A Av            0 cos 流量 二、概念及性质

(2) 设稳定流动的不可压缩流体（假定密度为1） 的速度场由 (x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k 给出，Σ是速度场中的一片有向曲面，函数 P(x,y,),Q(x,y,z),R(x,y,z) 都在Σ上连续，求在单位 时间内流向Σ指定侧的流 体的质量Φ

(2) 设稳定流动的不可压缩流体(假定密度为 1) 的速度场由 v x y z P x y z i Q x y z j R x y z k     ( , , )  ( , , )  ( , , )  ( , , ) 给出,Σ 是速度场中的一片有向曲面,函数 P( x, y,z), Q( x, y,z), R( x, y,z) 都在 Σ 上连续, 求在单位 时间内流向 Σ 指定侧的流 体的质量. x y z o 

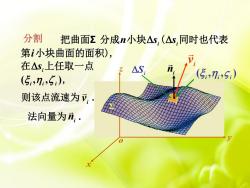
分割 把曲面Σ分成n小块△s,(△s,同时也代表 第i小块曲面的面积)， 在△S,上任取一点 子△S (5,7,5), (5,135) 则该点流速为立，· 法向量为元·

x y z o   Si ( , , ) i i i    i v  ni  把曲面Σ 分成n小块 i s ( i s 同时也代表 第i小块曲面的面积), 在 i s 上任取一点 ( , , )  i i  i , 分割 则该点流速为 . i v  法向量为 . ni 

=(5,7,5) =P(5,n,5)i+2(5,n,5)j+R(5,n,5)k, 该点处曲面Σ的单位法向量 n=cosa,i+cosBj+cosy,k, 近似求和通过△S,流向指定侧的流量近似值为 可·△S,(i=1,2,.,m. 通过Σ流向指定侧的流量 D≈∑可AS

该点处曲面Σ 的单位法向量 ni i i i j ik     cos cos  cos 0    , 0 ( 1,2, , ). i i i v n S i n    ( , , ) ( , , ) ( , , ) , ( , , ) P i Q j R k v v i i i i i i i i i i i i i                     近似求和 0 1 n i i i i v n S       通过Si流向指定侧的流量近似值为 通过Σ流向指定侧的流量

=∑IP(5i,n,5,)c0sa,+0(5,n,5:)cos月 +R(,5:)cosY;lAS, =∑IP(5,n,5△S,)R+2(5,5AS)x i- +R(5,7,5)△S)x 取极限入→0时取极限得到流量Φ的精确值. D=21P55as)+05,5》 +R(5,7,5)(△S)g]

1 [ ( , , )cos ( , , )cos ( , , )cos ] n i i i i i i i i i i i i i i P Q R S                   ( , , )( ) ] [ ( , , )( ) ( , , )( ) 1 i i i i x y yz i i i i x z n i i i i i R S P S Q S                  取极限    0 . 时取极限得到流量 的精确值 ( , , )( ) ] lim [ ( , , )( ) ( , , )( ) 1 0 i i i i x y yz i i i i x z n i i i i i R S P S Q S                    

2、概念 定义设Σ为光滑的有向曲面，函数在Σ上有 界，把∑分成n块小曲面△S:(△S,同时又表示第i 块小曲面的面积)，△S,在x0y面上的投影为 (△S)xy,(5,7,5i)是△S,上任意取定的一点，如 果当各小块曲面的直径的最大值入→0时， Iim∑R(5,n,5)(△S:)w →0=1 则称此极限为函数R(x,y,z)在有向曲面Σ上 对坐标xy的曲面积分（也称第二类曲面积分）

定义 设 Σ 为光滑的有向曲面,函数在 Σ 上有 界,把 Σ 分成n块小曲面Si (Si同时又表示第i 块小曲面的面积), Si 在 xoy 面上的投影为 Si xy ( ) ,( , , )  i i  i 是Si上任意取定的一点,如 果当各小块曲面的直径的最大值  0时,    n i R i i i Si xy 1 0 lim ( , , )( )  则称此极限为函数R(x, y,z)在有向曲面Σ 上 对坐标 x,y 的曲面积分(也称第二类曲面积分) 2、概念

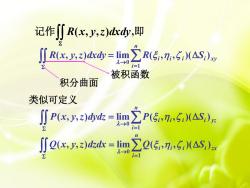
记作∬R(x,y,z)dcd,即 JRs3=m∑R(5,n:5,XASw i=1 被积函数 积分曲面 类似可定义 J∬P(c,yz)ddt=lim∑P(5n,5,(△S,)e →0 i1 (x,z)tkk=lm∑0(5，n,5,(△S)a 2→0 i=1

记作  R( x, y,z)dxdy,即       n i R i i i Si x y R x y z dxdy 1 0 ( , , ) lim ( , , )( )  被积函数 积分曲面 类似可定义       n i P i i i Si yz P x y z dydz 1 0 ( , , ) lim ( , , )( )        n i Q i i i Si zx Q x y z dzdx 1 0 ( , , ) lim ( , , )( ) 