《高等数学》课程教学资源（课件讲稿）第八章_8.2数量积与向量积

第二节数量积和向量积 ·一、两向量的数量积 ·二、两向量的向量积 ·三、小结

第二节 数量积和向量积 • 一、两向量的数量积 • 二、两向量的向量积 • 三、小 结

一、两向量的数量积 实例一物体在常力F作用下沿直线从点M移动 到点M,以表示位移，则力F所作的功为 w=F‖|cos0(其中0为F与3的夹角) 启示 两向量作这样的运算，结果是一个数量， 定义向量a与b的数量积为a.b d.b=a‖b1cos0(其中0为i与b的夹角)

一物体在常力F  作用下沿直线从点M1移动 到点M2，以s 表示位移，则力F  所作的功为 W | F || s | cos    (其中 为F  与s 的夹角) 启示 a b | a || b | cos       (其中 为a  与b  的夹角) 实例 两向量作这样的运算, 结果是一个数量. 一、两向量的数量积 向量a 与b 的数量积为a b   定义 

a.b=allb cose d .b cos0=PrjB,lalcos0=Prja, .a.b=b|Prja-aPrjB. 结论两向量的数量积等于其中一个向量的模 和另一个向量在这向量的方向上的投影的乘积. 数量积也称为“点积”、“内积

a  b   a b | a || b | cos       | b | cos Pr j b, a      | a | cos Pr j a, b     a b b jba       | | Pr | a | Pr j b. a    数量积也称为“点积”、“内积”. 结论 两向量的数量积等于其中一个向量的模 和另一个向量在这向量的方向上的投影的乘积

关于数量积的说明： (1)dd=a2. 证0=0，∴.dd=a‖|cos0=a2. (2).b=0=→aLb. 证（台→）.万=0，当|≠0,1b≠0时， cs8=0,0=经a5 当或中至少有一个零向量，也可认为它们垂直. (白）a,0-交cs9=0 a.b=albcos=0

关于数量积的说明： (2) a  b  0    a b.   () a  b  0,    当| | 0,| | 0 , a b   时 cos  0, a b.     (1) | | . 2 a a a      () a b,     cos  0, a  b | a || b | cos  0.       0, | || | cos | | . 2 a a a a a      证      证   , 2  , 2    当a b 或 中至少有一个零向量，也可认为它们垂直

数量积符合下列运算规律： (1)交换律：d.b=6.a (2)分配律：(a+b)c=dc+b.d (3)若孔为数：(i=.(2)=(d.) 若2、4为数：(2a)(b)=2(d.b)

数量积符合下列运算规律： （1）交换律： a b b a    （2）分配律： ( ) a b c a c b c       （3）若  为数： ( ) ( ) ( )    a b a b a b      若  、  为数： ( ) ( ) ( )    a b a b   

向量的数量积是否满足消去律？ 注 向量的数量积不满足消去律，即在一般情况下， d.b=d.c,a≠0的b=c. 事实上， a.b=d.c,是说d(6-)=0.即i-c与垂直， 未必h-c=0. c(a.b)(c.a)b. 注 平行于c的向量平行于b的向量

向量的数量积不满足消去律, 向量的数量积是否满足消去律？ a b a c    , 注 b c.     事实上, a b a c,        是说 a b c    ( ) 0.即b c a  与 垂直, 未必b  c  0. 注 c(a b) (c a)b.         ?  平行于 c 的向量  b  ≠平行于 的向量 0   a  即在一般情况下

》下列命题是否正确 (①)a··a=a3错，等式左边没意义. (2)a(a-b=ab错. (3)(a.b2a21b2错. (4)(a+b)(a-b)=曰a-1bP对

下列命题是否正确 错, 错. 对. 3 (1)a  a  a | a | 等式左边没意义. 2 (2) ( ) | | a a b a b   2 2 2 (3)(a b) | a | | b | 错. 2 2 (4)(a  b)(a  b) | a |  | b |

例1. 证明三角形余弦定理 c2 a2+b2-2abcos0 证：如图.设 CB=a,CA=b,AB=c 则 c-a-b B |=(@五)=aa+i.方-2a-b =a+万-2 eos0 a=a,b=B,c=c c2 a2 b2 -2abcos0

A B C  a b c 例1. 证明三角形余弦定理 2 2 2 c a b ab    2 cos 证: 则 2 2 2 c a b ab    2 cos 如图 . 设 CB a CA b AB c    , , 2 c  ( ) ( ) a b a b      a a   b b  2a b 2 2    a b a b 2 cos a a b b c c    ,

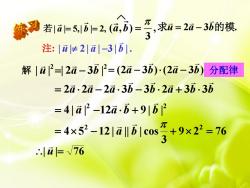
缘若1as12a,高)=子a=2a-36的模 注：|≠21-31b. 解|i2=2a-352=(2a-3b)(2a-3b)分配律 =2a.2a-2a.3b-3b.2a+3b.3i =41a-12d.6+9162 =4x5-121a61c0s+9x2=76 =√76

解 若| | 5,| | 2, a b   ( , ) , 3 a b   求 u 2 a 3 b的模.      注 : | u | 2 | a | 3 | b | .      | u |2 | 2a 3b |2 分配 律      (2a 3b) (2a 3 b)         a a a b b a b b          2  2  2  3  3  2  3  3 2 2 4 | a | 12a b 9 | b |         9 2 76 3 4 5 12 | || | cos 2 2        a b  | u | 76 

用向量的数量积，证明恒等式： |d+b2+1a-b2=2a2+21b2 即，平行四边形对角线的平方和等于四边的平方 和（如图）. -a+b 证1a+万2+1d-b2 a-b =(i+b)(a+b)+(a-b)(a-b) =a.a+2a.B+6.b+a.a-2a.b+b.b =2a2+262

用向量的数量积,证明恒等式: 即,平行四边形对角线的平方和等于四边的平方 和(如图). 证 2 2 2 2 | a b | | a b | 2 | a | 2 | b |            2 2 | a b | | a b |        (a b) (a b) (a b) (a b)                 a a a b b b a a a b b b                2       2    2 2 2 | a | 2 | b |     a  b  a b    a b   