《高等数学》课程教学资源（课件讲稿）第十章_10-4重积分的应用

第四节重积分的爱用 ·一、问题的提出 。二、曲面的面积 ·三、质心 ·四、转动横量 ·五、引力 ·六、小结

第四节 重积分的应用 • 一、问题的提出 • 二、曲面的面积 • 三、质心 • 四、转动惯量 • 五、引力 • 六、小结

一、问题的提出 把定积分的元素法推广到二重积分的应用中. 若要计算的某个量U对于闭区域D具有可加性 (即当闭区域D分成许多小闭区域是，所求量U相 应地分成许多部分量，且U等于部分量之和)，并 且在闭区域D内任取一个直径很小的闭区域do时， 相应的部分量可近似表示为f(x,y)dσ的形式， 其中(x,y)在D内.这个f(x,y)do就称为所求量U的 元素，记作dU,所求量U就可表示为积分 U=∬/x,yo

把定积分的元素法推广到二重积分的应用中. 一、问题的提出 ( ) ( , ) . ( , ( , ) ( , ) ) D U D D U U D d x y D f x y d U f x y d U f x y d dU U       若要计算的某个量 对于闭区域 具有可加性 即当闭区域 分成许多小闭区域是，所求量 相 应地分成许多部分量，且 等于部分量之和 ，并 且在闭区域 内任取一个直径很小的闭区域 时， 相应的部分量可近似表示为 的形式， 其中 在 内这个 就称为所求量 的 元素，记作 ，所求量 就可表示为积分

对三重积分而言 △U≈f(x,y,z)dw→dU=f(x,Jy,z)lw U=Jj川fx,yz)d Ω 1.平面图形的面积 由二重积分的性质，当x,y)=1时 区域D的面积A=∬do 2.空间立体的体积 设曲面的方程为z=f(x,y)≥0，(x,y)∈D

     dv x y z dv , ( , , )     U f x y z dv dU f x y z dv ( , , ) ( , , ) U f x y z dv ( , , )    1.平面图形的面积 由二重积分的性质，当 f( x, y ) =1 时 区域D的面积 D A d    2.空间立体的体积 设曲面的方程为 z f x y x y D    ( , ) 0,( , ) 对三重积分而言

则曲顶柱体的体积为V=∬fx,)o D 由三重积分的物理意义知空间闭区域Ω的体积为 =∬ 例1求z=2-x2-y2,z=x2+y2所围成的立体的体积 解一2在底面的投影为D:x2+y2=1 v=,-=∬2-x-yao-x+yao =21-如=可0-pp=x

则曲顶柱体的体积为 ( , ) D V f x y d    由三重积分的物理意义知空间闭区域  的体积为 V dv    所围成的立体的体积 2 2 2 2 求 z x y z x y      2 , 解一 2 2 2 2 2 1 (2 ) ( ) D D V V V x y d x y d            2 2 2 (1 ) D    x y d  2 1 2 0 0 2 (1 ) d d            例1 2 2    在底面的投影为D x y ： 1

解二在D上取一小区域do,它对应的柱体的的体积为 dW=(2-x2-y2-x2-y2)do 所以r=∬2-x2-Jy2-x2-yaa 解三 2是柱形区域，用柱坐标 r-了ajop订t 2元 2- =2xp(2-2pdp=

解三  是柱形区域，用柱坐标 V dv    2 2 2 1 2 0 0 d d dz            1 2 0    2 (2 2 )      d  解二 在D d 上取一小区域  ,它对应的柱体的 体积为 2 2 2 2 dV x y x y d      (2 )  2 2 2 2 (2 ) D V x y x y d       所以   

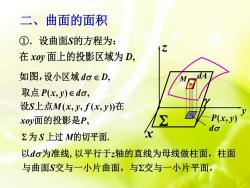
二、曲面的面积 ①.设曲面S的方程为： 在xOy面上的投影区域为D, 如图，设小区域do∈D, 取点P(x,y)∈do, 设S上点M(x,f(x,y)在 xOy面的投影是P, -P(x,y) do ∑为S上过M的切平面. 以do为准线，以平行于轴的直线为母线做柱面，柱面 与曲面S交与一小片曲面，与交与一小片平面

①．设曲面S的方程为： z f x y  ( , ) 在 xoy D 面上的投影区域为 , 取点 P x y d ( , ) ,   如图， 设小区域 d D   ,  为 S M 上过 的切平面. 二、曲面的面积 dP x y ( , ) M dA x y z s  o  ( , , ( , )) , S M x y f x y xoy P 设 上点 在 面的投影是 d z S   以 为准线,以平行于 轴的直线为母线做柱面，柱面 与曲面 交与一小片曲面，与 交与一小片平面

由于dσ很小，切平面Σ的小片平面面积A可以 代替相应的那小片曲面的面积. 设点M处曲面S上的法线（指向朝上）与z轴的 所成的角为y, .do为dA在xoy面上的投影， ∴.do=dA.cosy, 1 cosy= 1+f+f .dM=1+f经+fdo 曲面S的面积元素 以dσ为准线，以平行于z轴的直线为母线做柱面，柱面 与曲面交与一小片曲面，与交与一小片平面

曲面S的面积元素 由于d dA 很小,切平面的小片平面 积 可以 代替相应的那小片曲面的 积. M S z ( )  设点 处曲面 上的法线 指向朝上 与 轴的 所成的角为 ， d dA xoy  为 在 面上的投影,    d dA   cos , 2 2 1 cos , 1 x y f f     2 2 1 x y     dA f f d d z S   以 为准线,以平行于 轴的直线为母线做柱面，柱面 与曲面 交与一小片曲面，与 交与一小片平面

同理可得 ②.设曲面的方程为：x=g(y,) 曲面面积公式为：A=J∬V1+g,2+g:2d; D ③.设曲面的方程为：y=h(亿，x) 曲面面积公式为：A=小V1+:2+hk水

②．设曲面的方程为： x g y z  ( , ) 曲面面积公式为： 2 2 1 ; yz y z D A g g dydz     ③．设曲面的方程为： y h z x  ( , ) 曲面面积公式为： 2 2 1 . zx z x D A h h dzdx     同理可得

例2求球面x2+y2+z2=2含在圆柱体 x2+y2=c内部的那部分面积. 有对称性知A=44 解 D,:x2+Jy2≤x,(,y20) 曲面的方程为z=Va2-x2-y2 于*8- A=4∬V1+:2+z

解 2 2 1 D x y ax x y : , ( , 0)    曲面的方程为 2 2 2 2 2 2 2 . x y z a x y ax      例 求球面 含在圆柱体 内部的那部分面积 1 有对称性知A A  4 2 2 2 z a x y    2 2 2 2 2 1 , z z a x y a x y                     于是 1 2 2 4 1 x y D     A z z dxdy  o x y z a

-dxdy =nieG云pr- 例3求半径为R的球面的表面积 解 曲面方程为z=√R2-x2-y A=8A,=8V1+2+ (由对称性) =4πR2

1 2 2 2 4 D a dxdy a x y     2 cos 0 0 2 2 1 4 a a d d a           2 2   2 4 .  a a 求半径为R的球面的表面积 解 曲面方程为 （由对称性） 1 2 2 1 8 8 1 x y D A A z z dxdy      1 2 2 2 8 D R dxdy R x y     2 2 2 0 0 8 R R d d R          2  4 R 例3 2 2 2 z R x y   