《高等数学》课程教学资源（课件讲稿）第十二章_12.7傅里叶级数

第七节傅里叶级数 ·一、三角高数、三角岛数素的正交性 ·二、岛教展开成傅里叶级数 ·三、正程和余弦级数 四、小结 练习题

第七节 傅里叶级数 • 一、三角函数、三角函数系的正交性 • 二、函数展开成傅里叶级数 • 三、正弦和余弦级数 • 四、小结 练习题

一、三角级数三角函数系的正交性 简单的周期运动：y=Asin(ot+p)(谐波函数) (A为振幅，o为角频率，p为初相) 复杂的周期运动：y=A,+∑A,sin(not+9n) n= (谐波迭加) A sin o cos not+A coso sin not o=Ao a =Aa sin gn b=A.cost=x 得函数项级数 受+2a,osmx+6,mm) 称上述形式的级数为三角级数

一、三角级数 三角函数系的正交性 简单的周期运动 : (谐波函数) ( A为振幅, 复杂的周期运动 : sin cos cos sin A n t A n t n n n n      令 sin , n n n a A   cos , n n n b A   得函数项级数 0 1 ( cos sin ) 2 n n n a a n x b n x      为角频率, φ为初相 ) (谐波迭加) 称上述形式的级数为三角级数

三角函数系 1,cosx,sinx,c0s2x,sin2x,.c0sx,sin nx,. 正交： 任意两个不同函数在[-π，x上的积分等于零. ∫cosnxd=0, sind0. (n=1,2,3,.)

1, cos x,sin x, cos 2 x,sin 2 x, cos n x,sin n x,  : [ , ] .   正交 任意两个不同函数在 上的积分等于零 cos  0,    nxdx sin  0,    nxdx 三角函数系 (n  1,2,3, )

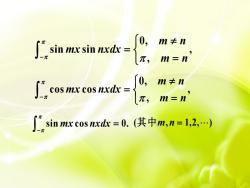
∫，sin mxsin nd= 0, m≠n , m=n ∫cos mx cos nd= 0, m≠n a,m=n' ∫sin mx cosd=0.(其中m,n=1,2,)

0 , sin sin , , m n mx nxdx m n           0 , cos cos , , m n mx nxdx m n           sin cos 0. mx nxdx     (其 中m,n  1,2, )

但是在三角函数系中两个相同的函数的乘积在[一π，π] 上的积分不等于0.且有 ∫1-1dx=2元 ∫cos2nxdx=元 (n=1,2,.) ∫sin2nxdx=元

上的积分不等于 0 . 1 1d 2 x        2 sin d n x x       2 cos d n x x       且有 但是在三角函数系中两个相同的函数的乘积在

二、函数展开成傅里叶级数 考虑以2π为周期的函数x)展开成三角级数的问题 问题：1.展开的条件是什么？ 2.若能展开，a,b:是什么？ 1.求系数ayb 复设e)=号+宫a,s+么如如 k1 (1)求a· (d +sin k)

二、函数展开成傅里叶级数 2.若能展开, ai ,bi 是什么? 问题：1.展开的条件是什么? 0 1 ( ) ( cos sin ) 2 k k k a f x a kx b kx   假设     (1) . 0 求a d x a k x b k x d x a f x d x k k k [ ( cos sin )] 2 ( ) 1 0                1. , i i 求 系 数 a b

2c+2a,cosk+2A,si血 0.2, 2 a,=∫fx)k (2)求an· )cosmdo coskxcossin kxcosnxdel h-

2 , 2 0    a 0 1 a f x dx ( )      d x a k xd x b kxdx a k k k k cos sin 2 1 1 0                     (2) . n 求a        nxdx a f x nxdx cos 2 ( )cos 0 [ cos cos sin cos ] 1           a k x nxdx  b k x nxdx k k k

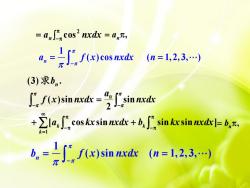
=anc0s2nxdk=a,元， a,=∫f(x)c c(n=1,2,3,) (3)求bn .f()sim-经innis cosndsine sin 6,=fx)sinm(u=1,23,）

    a nxdx n 2 cos  , n a 1 ( )cos ( 1, 2, 3, ) n a f x nxdx n       (3) . n 求b 1 ( )sin ( 1, 2, 3, ) n b f x nxdx n              nxdx a f x nxdx sin 2 ( )sin 0 [ cos sin sin sin ] 1           a kx nxdx  b kx nxdx k k k  , n b

()cos (-01 2.) 么=.sm,a=l2） 傅里叶系数 或 (e)cosue. 6=fx)s,a=l,2-

1 ( )cos , ( 0,1, 2, ) 1 ( )sin , ( 1, 2, ) n n a f x nxdx n b f x nxdx n                    2 0 2 0 1 ( )cos , ( 0,1, 2, ) 1 ( )sin , ( 1, 2, ) n n a f x nxdx n b f x nxdx n                或 傅里叶系数

傅里叶级数 an(a cosnx+bsinnx) 00 2 n=1 (2f(x)条件？号+∑(（a,eos+b,sinm) 00 2 n=1

傅里叶级数     1 0 ( cos sin ) 2 n an nx bn nx a 0 1 (2) ( ) ( co ) ? s sin 2 n n n a f x a nx b nx   条件   