《高等数学》课程教学资源（PPT课件）第一章 函数与极限_第十节 函数连续性习题课_连续性习题课

第十讲函数的连续性习题课

第十讲 函数的连续性习题课

函数的连续性习题课 一、内容小结 二、题型练习

函数的连续性习题课 一、内容小结 二、题型练习

函数的连续性习题课 一、内容小结 二、 题型练习

函数的连续性习题课 一、内容小结 二、题型练习

>连续的概念 定义 注意 优点 lim△y △x)0 三 Iim[f(x+△x)-f(x川=0 A是变量 直观、便于分析 左连续 lim f(x)=lim f(x)=f(xo) 三个要点 自然、便于应用 x→x6 右连续 Vε>0,3>0当x-xK6时 x可以等于x 清晰、便于论证 If(x)-f(x)Ks

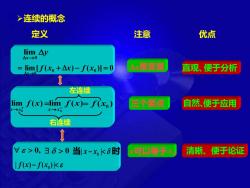
➢连续的概念 定义 注意 优点 y x   →0 limlim[ ( 0 ) ( 0 )] 0 0 = +  − =  → f x x f x x x 是变量 直观、便于分析 = → + lim ( ) 0 f x x x lim ( ) 0 f x x x → − ( ) x0 = f 左连续 右连续 三个要点 自然、便于应用    0,    0 当 | − |  0 x x 时 | ( )− ( )|  0 f x f x x 可以等于 x0 清晰、便于论证

>间断的概念与分类 ◆概念 (f(x)在x处没有定义 f(x)在x处有定义但1imfx)不存在 X→X0 、f（x)在x处有定义limf(x)存在 但imf(x)≠f(x,） x→x0 X→x ◆分类 可去间断点f(x)=f(x) 第一类间断点 f(x)和f(,)(跳跃间断点f(x对)≠f(x) 问断点 都存在 无穷间断点 第二类间断点 振荡间断点 f(x)和f(x) 至少一个不存在

➢间断的概念与分类 ◆概念 f (x) 在 x0 处没有定义 f (x) 在 x0 处有定义 lim ( ) 0 f x x→x f (x) 在 x0 处有定义 存在 lim ( ) 0 f x x→x 但 不存在 lim ( ) ( ) 0 0 f x f x x x  → 但 ◆分类 间断点 f (x0 + ) 和 ( ) − x0 f 都存在 第一类间断点 ( ) 和 + x0 f ( ) − x0 f 至少一个不存在 第二类间断点 ( ) ( ) + − 0 = x0 可去间断点 f x f ( ) ( ) + − 0  x0 跳跃间断点 f x f 无穷间断点 振荡间断点

>初等函数的连续性 连续函数经过四则运算仍连续 初等函数 连续函数经过复合运算仍连续 在其定义区间内连续 基本初等函数在定义域内连续 >闭区间上连续函数的性质 ◆有界性与最大值最小值定理 ◆零点定理与介值定理

➢初等函数的连续性 基本初等函数在定义域内连续 连续函数经过复合运算仍连续 连续函数经过四则运算仍连续 初等函数 在其定义区间内连续 ➢闭区间上连续函数的性质 ◆有界性与最大值最小值定理 ◆零点定理与介值定理

函数的连续性习题课 、内容小结 二、 题型练习

函数的连续性习题课 一、内容小结 二、题型练习

函数的连续性习题课 一、内容小结 二、 题型练习

函数的连续性习题课 一、内容小结 二、题型练习

二 题型练习 (一) 擗析题 (二) 间断点的判定 (三)分段函数的连续性 (四)确定常数 (五)证明题

二、题型练习 （一）辨析题 （二）间断点的判定 （三）分段函数的连续性 （四）确定常数 （五）证明题

二、题型练习 (一) 辨析题 (二)间断点的判定 (三)分段函数的连续性 (四)确定常数 (五)证明题

二、题型练习 （一）辨析题 （二）间断点的判定 （三）分段函数的连续性 （四）确定常数 （五）证明题