《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用_第一节 微分中值定理_微分中值定理

第一讲 微分中值定理

第一讲 微分中值定理

微分中值定理 一、罗尔定理 二、 拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

微分中值定理 罗尔定理 二、 拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

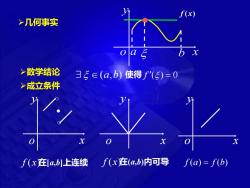
>几何事实 >数学结论 3飞∈(a,b)使得f'(5)=0 >成立条件 f(x在a,b]上连续 f(x在(a,b)内可导 f(a)=f(b)

➢几何事实 x y o a  b  (a,b) 使得 f () = 0 f (x) 在[a,b]上连续 f (x) 在(a,b)内可导 f (a) = f (b) x y o x y o x y o ➢数学结论 ➢成立条件 f (x)

>定理 如果函数x)满足 (1)在闭区间a,b1上连续 (2)在开区间(a,b)内可导 (3)在区间端点处函数值相等，即fa)=fb) 那么在(4，b)内至少有一点5(a证明思略 费马引理 设函数/y)在点xo的某 (x) 邻域Uo)内有定义，井 闭区间上 且在x。处可导，如果对 连续函数 任意的r∈Uo),有 的性质 fx)sf八xo) (回或 fw)≥o),那么 xo)=0

x y o a  b f (x) 如果函数f(x)满足 ➢定理 (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (3)在区间端点处函数值相等,即f(a)=f(b) 那么在(a,b)内至少有一点   ( ), a b   使得 f ( ) 0  = ➢证明思路 费马引理 设函数f(x)在点x0的某 邻域U(x0 )内有定义,并 且在x0处可导,如果对 任意的x∈U(x0 ),有 f(x)≤f(x0 ) (或 f(x)≥f(x0 )), 那么f '(x0 )=0 闭区间上 连续函数 的性质

●注 1.定理的条件是重要的 (1)条件不满足结论有可能不成立 (2)条件不满足结论也有可能成立 x2 x<1 例f(x)= 0 -2≤x≤-1 1 1≤x≤2 2.定理的条件是充足的 例f(x)=V1-x2

⚫注 1．定理的条件是重要的 （1）条件不满足结论有可能不成立 （2）条件不满足结论也有可能成立        −   −  = 1 1 2 0 2 1 1 ( ) 2 x x x x 例 f x x y o 2．定理的条件是充足的 例 2 f (x) = 1− x x y o

微分中值定理 罗尔定理 二、 拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

微分中值定理 罗尔定理 二、 拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 四、中值定理的应用

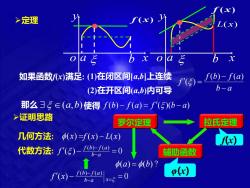
>定理 (x) (x) b x oag b x 如果函数fx)满足：(1)在闭区间a,b]上连续 f5)=6-1a) (2)在开区间(4，b)内可导 b-a 那么35∈(a,b)使得f(b)-f(a)=f'(5)b-a) >证明思路 罗尔定理 拉氏定理 几何方法： (x)=f(x)-L(x) fx) 代数方法：f(5)-1@=0 b-a 辅助函数 (a=b)? f(x)-1(b)-f(a) =5=0 p() b-a

a  b x y o f (x) x y o a  b f (x) 如果函数f(x)满足: ➢定理 (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 ➢证明思路 罗尔定理 拉氏定理 辅助函数 f(x) φ(x) (a) =(b) ? L(x) 几何方法: (x) =f (x) − L(x) 代数方法: ( ) 0 ( ) ( )  − = − − b a f b f a f  ( ) 0 ( ) ( )  − = = − − b a x  f b f a f x b a f b f a f − −  = ( ) ( ) ( ) 那么  (a,b) 使得 f (b) − f (a) = f ()(b − a)

●注 1与罗尔定理的关系 推广 罗尔定理 特例 拉氏定理 2.定理结论的其它形式 f(x2)-f(x)=f'(5)x32-x) ξ在x2与x1之间 fx1+△x)-f(x)=f'(5)△x ξ在x,与x+△x之间 f(x1+△x)-f(x)=f'(x1+△x)△x0<O<1 有限增量公式

⚫注 1．与罗尔定理的关系 罗尔定理 拉氏定理 推 广 特 例 2．定理结论的其它形式 ( ) ( ) ( )( ) 2 1 2 1 f x − f x = f   x − x ξ在x2与x1之间 f (x + x) − f (x ) = f ( )x 1 1  ξ在x1与x1+Δx之间 f (x1 + x) − f (x1 ) = f (x1 +x)x 0  1 有限增量公式