《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用_第八节 函数图形的描绘_函数图形的描绘

第八讲逯数图形的描绘

第八讲 函数图形的描绘

函数图形的描绘 一、函数的性态 二、函数图形的描绘

函数图形的描绘 一、函数的性态 二、函数图形的描绘

函数图形的描绘 丞数的性态 二、函数图形的描绘

函数图形的描绘 一、函数的性态 二、函数图形的描绘

>函数的性态 特性 性态 研究工具 关键点 定义域 自变量变化范围 无定义的点 整 值域 函数取值范围 初等方法 体 奇偶性 图形的对称性 有 周期性 图形的平移性 限 连续性 图形的连续性 极限 间断点、零点 局 单调性 图形的升降 一阶导数 极值点 二阶导数 拐点 无 凸凹性 图形的弯曲方向 限 渐近线 图形的变化趋势 极限

➢函数的性态 特性 性态 关键点 定义域 自变量变化范围 值域 函数取值范围 奇偶性 图形的对称性 周期性 图形的平移性 单调性 图形的升降 凸凹性 连续性 图形的连续性 图形的弯曲方向 渐近线 图形的变化趋势 研究工具 初等方法 极限 一阶导数 二阶导数 极限 无定义的点 间断点、零点 极值点 拐点 整 体 局 部 有 限 无 限

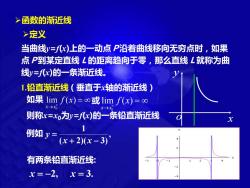
函数的渐近线 >定义 当曲线=八x)上的一动点P沿着曲线移向无穷点时，如果 点P到某定直线L的距离趋向于零，那么直线L就称为曲 线y三fx)的一条渐近线。 1铅直渐近线（垂直于x轴的渐近线） 如果limf(x)=∞或1imf(x)=o∞ 则称x=xo为y=f孔x)的一条铅直渐近线 例如y= 1 (x+2)(x-3) 有两条铅直渐近线： x=-2, x=3

0 lim ( ) x x f x → + 如果 =  或 0 lim ( ) x x f x → − =  ➢定义 1.铅直渐近线 当曲线y=f(x)上的一动点Ｐ沿着曲线移向无穷点时，如果 点Ｐ到某定直线Ｌ的距离趋向于零，那么直线Ｌ就称为曲 线y=f(x)的一条渐近线。 （垂直于x轴的渐近线） 则称x=x0为y=f(x)的一条铅直渐近线 ➢函数的渐近线 x y o 例如 , ( 2)( 3) 1 + − = x x y 有两条铅直渐近线: x = −2, x = 3

2.水平渐近线（平行于x轴的渐近线） 如果limf(x)=b或limf(x)=b 则称y=b为y=孔x)的一条水平渐近线 例如 y=arctanx, 有两条水平渐近线： 元 0 y=2y=- -15 -10 5 -0

2.水平渐近线（平行于x轴的渐近线） 例如 y = arctanx, 有两条水平渐近线: . 2 , 2  = −  y = y 如果 lim ( ) x f x b →+ = lim ( ) x f x b →− 或 = 则称y=b为y=f(x)的一条水平渐近线 x y o

3.斜渐近线 如果1im[f(x)-(ax+b)】=0或1im[f(x)-(ax+b)小=0 （a,b为常数)则称=x+b为=fx)一条斜渐近线 >斜渐近线求法： a lim f(x) b=lim[f(x)-ax] X-→00 ●注 如果 (1)im f(x) 不存在 x→o0 (2)im x→0 x=a存在，但imf(x)-]不存在 则=fx)不存在斜渐近线

3.斜渐近线 ➢斜渐近线求法: ( ) lim , x f x a → x = lim[ ( ) ] x b f x ax → = − 如果 lim [ ( ) ( )] 0 x f x ax b →+ − + = 或 lim [ ( ) ( )] 0 x f x ax b →− − + = （a,b为常数） 则称y=ax+b为y=f(x)一条斜渐近线 ⚫注 如果 ( ) (1) lim x f x → x 不存在 ( ) (2) lim x f x a → x = 存在，但 lim[ ( ) ] x f x ax →  − 不存在 则y=f(x)不存在斜渐近线

lim (x) b =lim[f(x)-ax] X→00 X ◆例1 求) 2(x-2x+3 的渐近线 x-1 解D:(-o,1U(1,+o).·.limf(x)=-oo, lim f(x)=+0, x-> .∴x=1是曲线的铅直渐近线 又lim f(x) 2(x-2)(x+3) lim =2 x→0 X→00 x(x-1) 100 lim 2(x-2)(x+3) -2x] 50 x→00 (x-1) 4 lim 2(x-2)(x+3)-2x(x-1) 二4， -50 X→00 x-1 -100 .'y=2x+4是曲线的一条斜渐近线

解 D :(−,1)(1,+). ◆例1 求 2( 2)( 3) ( ) 1 x x f x x − + = − 的渐近线 ( ) lim , x f x a → x = lim[ ( ) ]. x b f x ax → = − 1 lim ( ) , x f x → + = − 1 lim ( ) , x f x → − = + ∴x=1是曲线的铅直渐近线 ( ) 2( 2)( 3) lim lim 2, ( 1) x x f x x x → → x x x − + = = − 又 2( 2)( 3) lim[ 2 ] ( 1) x x x x →  x − + − − 2( 2)( 3) 2 ( 1) lim 4, x 1 x x x x →  x − + − − = = − ∴y=2x+4是曲线的一条斜渐近线

函数图形的描绘 数的性态 二、函数图形的描绘

函数图形的描绘 一、函数的性态 二、函数图形的描绘

函数图形的描绘 级数的性态 二 拯数图形的描绘

函数图形的描绘 一、函数的性态 二、函数图形的描绘