《高等数学》课程教学资源（PPT课件）第七章 微分方程_第二节 一阶线性微分方程_一阶线性微分方程

第二讲 一阶线性微分方程

第二讲 一阶线性微分方程

一 阶线性微分方程 一、一阶线性微分方程 二、伯努利方程

一阶线性微分方程 一、一阶线性微分方程 二、伯努利方程

阶线性微分方程 一、一阶线性微分方程 二、伯努利方程

一阶线性微分方程 一、一阶线性微分方程 二、伯努利方程

一、一阶线性微分方程 (一)类型与解法 (二) 举例

一、一阶线性微分方程 （一）类型与解法 （二）举例

一 阶线性微分方程 (一）类型与解法 (二)举例

一、一阶线性微分方程 （一）类型与解法 （二）举例

>一阶线性微分方程 +P(x)y=Q(x) dx 特点：关于y为线性（一次式） 例：y'+2y=0 y'+x"y=sinx y'+xy2=sinx (y')2+xy=sinx③ dy y dx x+y dx x+y dy 〔Q(x)=0 齐次的 分类 2(x)≠0— 非齐次的

( ) ( ) d d P x y Q x x y + = 非齐次的 齐次的 ➢一阶线性微分方程 特点：关于y′y为线性（一次式） 例： y xy  + = 2 0 2 y x y x  + = sin 2 y xy x  + = sin 2 ( ) sin y xy x  + = 分类： Q x( ) 0 = Q x( ) 0  4 d d x y y x y + = y x y y x 4 d d + =

>解法 齐次方程 dy+P(x)y=0 d ↓ 分离变量 dy =-P(x)dx y 两边积分 In y =-P(x)dx+In C 通解 y=Ce

( ) 0 d d + P x y = x y 分离变量 两边积分 ln y = − P(x)dx + ln C 通解 ➢解法 齐次方程  = − P x x y C ( )d e

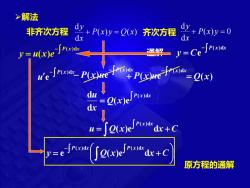
>解法 非齐次方程 +P(x)y=Qx)齐次方程 dx 少y+Pxy=0 dx y=mx)e y=Ce∫Pa u'e-ro P(x) =C(x) [P(x)dx dx u=fQ(x)ex+C =eJregelra+c 原方程的通解

( ) 0 d d + P x y = x y 通解 ➢解法 非齐次方程 ( ) ( ) 齐次方程 d d P x y Q x x y + = 原方程的通解  = − P x x y C ( )d e  = − P x x y u x e ( )d ( )   − P x x u ( )d e  − − P x x P x u ( )d ( ) e + P(x)  − P x x u ( )d e = Q(x)  = P x x Q x x u ( )d ( )e d d  +  u = Q x x C P x x ( )e d ( )d       +   =  − y Q x x C P x x P x x e ( )e d ( )d ( )d

一 阶线性微分方程 (一)类型与解法 (二)举例

一、一阶线性微分方程 （一）类型与解法 （二）举例

一 、一阶线性微分方程 (一) 类型与解法 (二) 举例

一、一阶线性微分方程 （一）类型与解法 （二）举例