《高等数学》课程教学资源（PPT课件）第九章 多元函数的微分法及其应用_第四节 多元函数极本概念习题课_习题课

第四讲 多元拯数微分学概念习题课

第四讲 多元函数微分学概念习题课

多元函数微分学概念习题课 一、内容小结 二、题型练习

多元函数微分学概念习题课 一、内容小结 二、题型练习

多元函数微分学概念习题课 一、内容小结 二、题型练习

多元函数微分学概念习题课 一、内容小结 二、题型练习

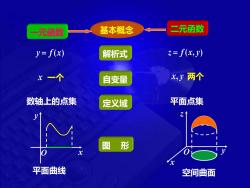
元函数 基本概念 二元函数 y=f(x) 解析式 z=f(x,y) x一个 自变量 x,y两个 数轴上的点集 定义域 平面点集 图 形 平面曲线 空间曲面

一元函数 基本概念 二元函数 y = f (x) 解析式 z = f (x, y) x 一个 自变量 x, y 两个 数轴上的点集 定义域 平面点集 图 形 O x y x O z y 平面曲线 空间曲面

元函数 基本概念 二元函数 limf(x)=A之 lim f(x,y)=A x→x0 极 限 (x,xn】 f(x)=f(x)=A 任何路径的极限都等于A lim f(x)=f(x) 连 续 imf(化，y)=f(xo,yo) x->xo (xJx%）】 f(xo,Yo)= f"(x)=lim f(x,+△x)-f(x, △x-0 △Y (偏)导数 lim f(x+△x,yo)-f(x,Jy） △x→0 △x ffyfrFo f"(x) 高阶导数 混合偏导数连续时相等 dy=f(x)dx (全)微分 dz= 0 d此+ dy Ox a

一元函数 基本概念 二元函数 极 限 连 续 (偏)导数 (全)微分 高阶导数 f x A x x = → lim ( ) 0 f x y A x y x y = → lim ( , ) ( , ) ( , ) 0 0 f x = f x = A + − ( ) ( ) 0 0 任何路径的极限都等于A lim ( ) ( ) 0 0 f x f x x x = → lim ( , ) ( , ) 0 0 ( , ) ( , ) 0 0 f x y f x y x y x y = → x f x x f x f x x  +  −  =  → ( ) ( ) ( ) lim 0 0 0 f x (x0 , y0 ) = x f x x y f x y x  +  −  → ( , ) ( , ) lim 0 0 0 0 0 f (x) f xx , f xy , f yx , f yy ,  混合偏导数连续时相等 dy = f (x)dx y y z x x z dz d d   +   =

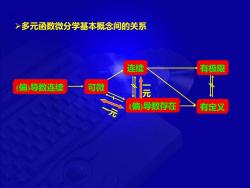
>多元函数微分学基本概念间的关系 连续 有极限 (偏)导数连续 可微 (偏)导数存在 有定义

➢多元函数微分学基本概念间的关系 (偏)导数连续 可微 (偏)导数存在 连续 有极限 有定义 一 元

多元函数微分学概念习题课 一、内容小结 二、题型练习

多元函数微分学概念习题课 一、内容小结 二、题型练习

多元函数微分学概念习题课 一、内容小结 二、 题型练习

多元函数微分学概念习题课 一、内容小结 二、题型练习

◆例1设fx-y,hx)=1-当)，e xe'h(x) 求f(x,y以 ◆例2设f(x,y)=x+2y,求f(y,f(化，y) ◆例3求下列函数的定义域，并画草图 (1)=lnx(x-y)] (2)z=4y-x2-y2+x2+y2-2 (3)u= :x2+y arcsin- (补)z=U-xW2x-y] 2 ◆例4求下列极限 ().im（x2+y2)sin (2)1im sin(2yy)） (x,)→(0,0) (x→0，a4）y x2+ (3) lim (4) limx23y2m(x2+y2） x,→0,0)x|+|y (x,y→0,0)

◆例1 ◆例3 设 , e ln( ) e ( ,ln ) (1 ) y x x x x y f x − y x = − 求 f (x, y). ◆例2 设 f (x, y) = x + 2y, 求 f (xy, f (x, y)). 求下列函数的定义域,并画草图 (1) z = ln[ x(x − y)] (2) z 4 y x y x y 2 y 2 2 2 2 = − − + + − (3) z x y u 2 2 arcsin + = (补) z = ln[( y − x) 2x − y] ◆例4 求下列极限 (1) xy x y x y 1 lim ( )sin 2 2 ( , ) (0,0) + → (2) y xy x y a sin(2 ) lim ( , )→(0, ) (3) | | | | lim 2 2 ( , ) (0,0) x y x y x y + + → (4) lim ln( ) 2 2 2 2 ( , ) (0,0) x y x y x y + →

◆例5证明下列极限不存在 (少，lim (2) x2+y2 lim (x,y→0,0)x+y 0,01+(x-y)月 (3) lim In(1+x) c0.0x2y2+(x-y (4) lim x→0,0)x+tany ◆补1 证明极限m. a(心2+不存在 sin xy y1+x2) y≠0 ◆例刚6研究函数k,)= 在(0,0)的连续性 y=0 xsin(x-2y) x≠2y ◆刚7设/x= x-2y ,求f(x,y)的间断点. x=2y

◆例5 证明下列极限不存在 (1) x y xy ( x, y)→(0,0) + lim (2) 4 2 2 ( , ) (0,0) 1 ( ) lim x y x y x y + − + → (3) 2 2 2 2 2 ( , ) (0,0) ( ) lim x y x y x y x y → + − (4) x y xy x y tan ln(1 ) lim ( , ) (0,0) + + → ◆补1 证明极限 2 4 3 4 4 ( , ) (0,0) ( ) lim x y x y x y → + 不存在. ◆例6 研究函数 = (0,0) 的连续性. f (x, y) (1 ) sin 2 y x xy + y  0 0 y = 0 在 ◆例7 设 f (x, y) = x y x x y 2 sin( 2 ) − − x  2 y 0 x = 2 y ，求 f (x, y) 的间断点