《高等数学》课程教学资源（PPT课件）第八章向量代数与空间解析几何_第二节 数量积与向量积_数量积与向量积

第二讲数量积向量积

第二讲 数量积 向量积

数量积向量积 两向量的数量积 二、两向量的向量积

数量积 向量积 一、两向量的数量积 二、两向量的向量积

数量积向量积 两向量的数量积 二、两向量的向量积

数量积 向量积 一、两向量的数量积 二、两向量的向量积

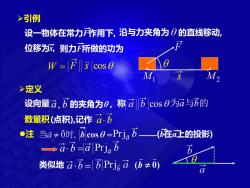
>引例 设一物体在常力F作用下，沿与力夹角为日的直线移动， 位移为，则力所做的功为 w =Fs coso ~e M M, >定义 设向量a,b的夹角为9，称abcos0为a与b的 数量积（点积），记作a,b ●注当a≠0时，bcos0=Prja B一（在a让的投影） ->a.b=a Prjab 类似地a.乙=bPrj5a(b≠0)

M1 W =  ➢定义 F s cos  M2 a b 设向量 的夹角为 , 称 数量积(点积),记作 a, b 为a与b的 s ➢引例 设一物体在常力F作用下, 沿与力夹角为 的直线移动, 位移为s, 则力F所做的功为  ⚫注 Prja  b a b = a Prja  b ( 0)   类似地 b  (b在a上的投影)

>性质 (1)a.a-ap (2)a,b为两个非零向量，则有a方=0←→a16 >运算律 (1)交换律 a.b-ba (2)结合律 (2,4为实数) (2a)b=a:(2b=2(a.b (Aa)(uB)=Au(a.B) Prjca Prje b (3)分配律 (a+b)c-a.c+b.c Prjz(@+B) ◆例1证明三角形余弦定理c2=a2+b2-2 ab cos0

➢性质 为两个非零向量, 则有 (1) a  a = (2) a,b a b = 0 ⊥ ➢运算律 (1)交换律 (2)结合律 a ( b) ( a)( b) =   (a b) (3)分配律 c a b + b a a Prj c  b c Prj Prj (a b) c  + ◆例1证明三角形余弦定理 2 cos . 2 2 2 c = a +b − ab 

>数量积的坐标表示 a=asi+ay j+ak,B=bi+by j+b k, a.B=(axi+ay j+azk)(bxi+by J+b-K) ↓i7=万=录=1,7j=jk=i=0 a.b=abx +ayby +a-b: 当a,b为非零向量时，a.b=abcos0 cos0 a.b axbx +arby +a-b a ja+a;ta2 ++b2 两向量夹角公式

➢数量积的坐标表示 设 = 0 x x y y z z =a b + a b + a b 当 为非零向量时, cos = = x x y y z z a b + a b + a b 2 2 2 ax + ay + az 2 2 2 bx + by + bz a b cos a a i a j a k , = x + y + z b b i b j b k , = x + y + z (a i + a j + a k ) x y z (b i b j b k ) x + y + z i  j = j  k = k i a b a b 两向量夹角公式

◆例2 已知三点M1,1,1),A(2,2,1),B2,1,2)A 求∠AMB ◆例3设均匀流速为的流体流过一个面积为4的 平面域，且与该平面域的单位垂直向量 的夹角为O,求单位时间内流过该平面域的 流体的质量P(流体密度为p)

◆例2 B M A M (1,1,1), A(2,2,1),B(2,1,2), 求 AMB . 已知三点 ◆例3  A 求单位时间内流过该平面域的 设均匀流速为 的流体流过一个面积为A的 平面域 , 与该平面域的单位垂直向量 的夹角为 且 流体的质量P(流体密度为)

数量积向量积 两向量的数量积 二、两向量的向量积

数量积 向量积 一、两向量的数量积 二、两向量的向量积

数量积向量积 两向量的数量积 二、 两向量的向量积

数量积 向量积 一、两向量的数量积 二、两向量的向量积

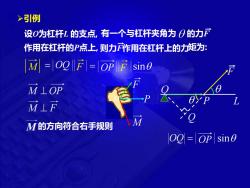
>引例 设O为杠杆L的支点，有一个与杠杆夹角为日的力F 作用在杠杆的P点上，则力F作用在杠杆上的力矩为： M=0QF1=oPF§ ine M⊥OP 应⊥F M的方向符合右手规则 M 00=Op sin0

设O为杠杆L 的支点, 有一个与杠杆夹角为 OQ = O P L   Q 的方向符合右手规则 = OQ F = OP F sin OP sin M M ⊥ OP M 作用在杠杆的P点上, 则力F作用在杠杆上的力矩为: F o P F M M ⊥ F ➢引例 的力F