《高等数学》课程教学资源（PPT课件）第九章 多元函数的微分法及其应用_第九节 方向导数与梯度_方向导数与梯度

第九讲方向导数与梯度

第九讲 方向导数与梯度

方向导数与梯度 一、方向导数 二、梯度

方向导数与梯度 一、方向导数 二、梯度

方向导数与梯度 一、方向导数 二、梯度

方向导数与梯度 一、方向导数 二、梯度

一、方向导数 (一) 定义 (二)计算

一、方向导数 （一）定义 （二）计算

一、方向导数 (一) 定义 (二) 计算

一、方向导数 （一）定义 （二）计算

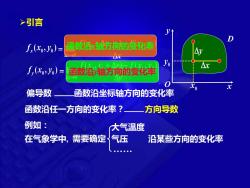
>引言 f:(XoXo)= 函数沿轴方向的变化率 J0 f,(x,)= 函数沿轴方向的变化率 偏导数 函数沿坐标轴方向的变化率 函数沿任一方向的变化率？一方向导数 例如： 大气温度 在气象学中，需要确定 气压 沿某些方向的变化率

➢引言 偏导数 ( , ) 0 0 f x y x x f x x y f x y x  +  − =  → ( , ) ( , ) lim 0 0 0 0 0 x y O D 0 x 0 y x 函数沿x轴方向的变化率 ( , ) 0 0 f x y y y f x y y f x y y  +  − =  → ( , ) ( , ) lim 0 0 0 0 0 y 函数沿y轴方向的变化率 函数沿坐标轴方向的变化率 函数沿任一方向的变化率？ 例如： 在气象学中, 需要确定 大气温度 气压 . 沿某些方向的变化率 方向导数

>引言 设u=f化，在PKJo,的某一邻域内有定义， 是以P,(x,J为起点的一条射线 =(Cosa,c0sB,c0sy）P(x,y,)是1上任点， PP=t(t≥0，PP∥→PP=店 x-x=y二h=名-=i cosa cosβcosy 射线1的参数方程： 〔x=x+tc0sa y=o+tcos B t≥0→P(x+tc0sa,y+tc0sB,z+tc0sY） =+tcosy

➢引言 设 在 ( , , ) 0 0 0 0 u = f (x, y,z) P x y z 的某一邻域内有定义, 是以 ( , , ) 0 0 0 0 l P x y z 为起点的一条射线 ) l P(x, y,z 是 上任一点, P0 P l e = (cos,cos  ,cos ) l e l P P = te 0 | | ( 0), P0 P = t t  t x x y y z z = − = − = − cos cos  cos 0 0 0 射线 l 的参数方程: x = x0 + t cos y = y0 + t cos cos 0 z = z + t t  0 ( cos , cos , cos ) 0 0 0 P x + t  y + t  z + t  P0 P l y x z O t

>定义 设u=f,J,2在P,(K,Jo的某一邻域U(,)内有定义，1是以 P(化o,Jyo,z为始点的一条射线，P(。+tc0sa,yn+tc0s阝，+tc0sY） 是I上另一点，且P∈U(P,),如果函数增量 f(x+tcosa,y+tcosB,to+tcosy)-f(xo>Vo,Zo) 与P到P的距离PP,=t的比值 f(x+tcosa,o+tcosB,to+tcosy)-f(xoYoZo) t 当P沿着趋于P,即1→0)时的极限存在，则称此极限为 函数f化，在P沿方向的方向导数，记作2I Ol (xo,%o,z0)

➢定义 设 在 ( , , ) 0 0 0 0 u = f (x, y,z) P x y z 的某一邻域 ( , , ) 0 0 0 0 P x y z 为始点的一条射线, 是 l 上另一点, ( cos , cos , cos ) 0 0 0 P x + t  y + t  z + t  U(P0 ) 内有定义, l 是以 ( ), 且 P U P0 如果函数增量 ( cos , cos , cos ) ( , , ) 0 0 0 0 0 0 f x + t  y + t  z + t  − f x y z 与 P 到 P0 的距离 | PP |= t 0 的比值 t f (x t cos , y t cos ,z t cos ) f (x , y ,z ) 0 + 0 + 0 + − 0 0 0    当 P 沿着l趋于 P0 (即 → + t 0 )时的极限存在，则称此极限为 函数 f (x, y,z) 在 P0 沿方向l的方向导数,记作 . ( , , ) 0 0 0 l x y z f  

●注()二元函数f(x,y在P(x,沿方向方向角为a,) 的方向导数为 of lim f(xo+tcosa,yo+tcosB)-f(xo,yo) a1 (xo,yo) 1-→0 (2) of 刻画了函数f(x,J》,)在（化，yo,) (X0,0,z） 沿方向的变化率 lim f(x+tcosa,yo+tcos B,to+tcosy)-f(xo,yo,zo OI (xo2Yo,zo) t-→0t

t f x t y t z t f x y z t ( cos , cos , cos ) ( , , ) lim 0 0 0 0 0 0 0 + + + − = → +    ( , , ) 0 0 0 l x y z f   ⚫注 二元函数 f (x, y) 在 ( , ) 0 0 0 P x y 沿方向l(方向角为 , ) 的方向导数为 t f x t y t f x y t ( cos , cos ) ( , ) lim 0 0 0 0 0 + + − = → +   ( , ) 0 0 l x y f   (1) (2) ( , , ) 0 0 0 l x y z f   刻画了函数 f (x, y,z) 在 ( , , ) 0 0 0 0 P x y z 沿方向l的变化率

单侧极限 ●注(3)定义式的特点 比式∫分子：射线上两点函数值之差 分母：射线1上两点的距离 (4)偏导数与方向导数 例 =i of =f(x） f(x,%)存在 al (xoy) lG=-i→0/ (,)-.(6) n-g-新o =1但f(0,0)不存在 lim f(xo+tcosa,yo+tcosB,to+tcosy)-f(xo>Yo,Zo) OI (xo,yo,Zo) -0

t f x t y t z t f x y z t ( cos , cos , cos ) ( , , ) lim 0 0 0 0 0 0 0 + + + − = → +    ( , , ) 0 0 0 l x y z f   ⚫注 (3) (4) ( , ) ( , ) 0 0 0 0 f x y l x y f = x   单侧极限 例 定义式的特点 比式 分子: 射线l上两点函数值之差 分母: 射线l上两点的距离 偏导数与方向导数 ( , ) 0 0 f x y x 存在, e i l = e i l = − ( , ) ( , ) 0 0 0 0 f x y l x y f = − x   2 2 f (x, y) = x + y e i l = 1 (0,0) =   l f (0,0) x 但 f 不存在