《高等数学》课程教学资源（PPT课件）第八章 向量代数与空间解析几何_8-2 数量积 向量积 混合积

第八章 第二节 数量积向量积*混合积 一、两向量的数量积 二、两向量的向量积 *三、向量的混合积

*三、向量的混合积 第二节 一、两向量的数量积 二、两向量的向量积 数量积 向量积 *混合积 第八章

两向量的数量积 引例.设一物体在常力F作用下，沿与力夹角为0 的直线移动，位移为了，则力F所做的功为 W=F‖3cos0 1.定义 M2 设向量a,b的夹角为0，称 记作 abcose ab W=F,5 为a与b的数量积（点乘积）

M1 一、两向量的数量积 沿与力夹角为 的直线移动,  W = 1. 定义 设向量 的夹角为 ,称 记作 数量积 (点乘积) . 引例. 设一物体在常力 F 作用下, 位移为 s , 则力F 所做的功为 F s cos  W F s  =  M2 a b 为a与b的 a, b s

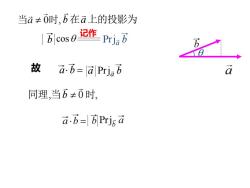
当a≠0时，b在a上的投影为 |6cos0记作prj,万 故 ab=a Priab 同理，当b≠0时， a.b=BPrjr a

 b 在a上的投影为   记作 故 同理,当 0 时,   b  b Prja b a b = a Prja b

2.性质 (1)a.a-ap (2)a,为两个非零向量，则有 ab=0=a⊥b

2. 性质 为两个非零向量, 则有 (1) a  a = (2) a,b a b = 0 ⊥

3.运算律 (1) 交换律a.b=b.d (2)结合律(2，u为实数) (b=a(b)=(a.b) (a).(ub)=a(a.(ub))=au(a.b) (3)分配律(a+b)c=d·c+bc

3. 运算律 (1) 交换律 (2) 结合律 a ( b) ( a)( b) =  ( a ( b)) =   (a b) (3) 分配律

例1.证明三角形余弦定理 c2 =a2+b2-2abcos0 证：如图.设 CB=a,CA=b,AB=c 则 c-a-b B c2=(a-瓦：(@-)=a+6-6-2a-b =|a2+62-2a6cos0 a=d,b=b,c=c创 c2 a2+b2-2abcose

A B C  a b c 例1. 证明三角形余弦定理 2 cos 2 2 2 c = a + b − ab 证: 则 2 cos 2 2 2 c = a + b − ab 如图 . 设 CB = a, CA = b, AB = c = 2 c (a −b)(a −b)= a  a + bb − 2a b 2 = a 2 + b − 2 a b cos a = a , b = b , c = c

4.数量积的坐标表示 设=axi+ayj+a.,b=bi+b,j+b.k,则 a.b=(axi+ay j+ak)(bs i+by j+b k) 7-示-双=1，可-方话=i-0 a·b=abx+aby+a,bs

4. 数量积的坐标表示 设 则 = 0 x x y y z z = a b + a b + a b a a i a j a k , = x + y + z b b i b j b k , = x + y + z (a i + a j + a k ) x y z (b i b j b k ) x + y + z i  j = j  k = k i a b

a.b=axbx +ayby +a-b- 两向量的夹角 当a,b为非零向量时，由于a·b=a‖bcos0,得 a.b c0S0= axbx +a,by +a-b= ab yata+a++b

x x y y z z =a b + a b + a b 当 为非零向量时, cos = = x x y y z z a b + a b + a b 2 2 2 ax + ay + az 2 2 2 bx + by + bz 由于 a b cos a b a b 两向量的夹角 , 得

例2.已知三点M(1,1,1),A(2,2,1),B(2,1,2), 求∠AMB 解：MA=(1,1,0),MB=(1,0,1) 则 COS∠AMB= MA·MB MAMB 1+0+01 √2V√2 2 故 ∠AMB= -3

MA = ( ), MB = ( ) = B M 例2. 已知三点 M (1,1,1), A(2,2,1),B(2,1,2),  AMB . A 解: 1, 1, 0 1, 0, 1 则 cos AMB = 1+0 +0 2 2 AMB = 求 MA  MB MA MB 故

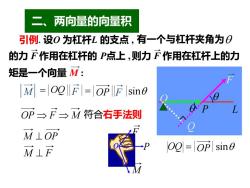
二、两向量的向量积 引例.设0为杠杆L的支点，有一个与杠杆夹角为O 的力F作用在杠杆的P点上，则力F作用在杠杆上的力 矩是一个向量M: M=0F=OpFsine OP三F三M符合右手法则 M⊥OP M⊥F 0Q=OP sin0

二、两向量的向量积 引例. 设O 为杠杆L 的支点 , 有一个与杠杆夹角为 OQ = O P L   Q 符合右手法则 = OQ F = OP F sin OP sin OP  F  M M ⊥ OP M 矩是一个向量 M : 的力 F 作用在杠杆的 P点上 ,则力 F 作用在杠杆上的力 F o P F M M ⊥ F