《概率论与数理统计》课程教学资源（PPT课件）2.2 离散型随机变量及其分布律

第二节离散型随机变量 及其分布律 一、离散型随机变量的分布律 二、常见离散型随机变量的概率分布

一、离散型随机变量的分布律 二、常见离散型随机变量的概率分布 第二节 离散型随机变量 及其分布律

一、离散型随机变量的分布律 定义设离散型随机变量X所有可能取的值为x(k=1,2,), X取各个可能值的概率，即事件{X=x}的概率为 P{X=x}=Pk,k=1,2,·. 称此式为离散型随机变量X的分布律. 注：分布律满足的两个条件： ∫四p≥0，k=1,2,. (2)∑p.=1. k_1 离散型随机变量的分布律也可表示为 Xx1x2.xn. P P1p2.Pm

( 1,2, ), , { } { } , 1,2, . . k k k k X x k X X P k x X X x p = = = = = 设离散型随机变量 所有可能取的值为 取各个可能值的概率 即事件 的概率为 称此式为离散型随机变量 的分布律 一、离散型随机变量的分布律 定义 注： 分布律满足的两个条件： (1) 0, 1,2, ; k p k  = 1 (2) 1. k k p  =  = X k p 1 2 n x x x 1 2 n p p p 离散型随机变量的分布律也可表示为

利用离散型随机变量X的分布律求事件的概率： 设离散型随机变量X的分布律为 P{X=x}=Pk,k=1,2,. L是一个实数集合，事件A=X∈L},则 P(o-pxen->px-s->p

L是一个实数集合，事件A= {X∈L}，则 利用离散型随机变量X 的分布律求事件的概率： 设离散型随机变量X的分布律为 P A P X L ( ) { } =  = { } k k x L P X x   = k k x L p  =  { } , 1,2,. P X x p k = = = k k

例如设离散型随机变量X的分布律为 X012345 131434 Pk 161616161616 则P{x≤2}=P{X=0}+P{X=1}+P{X=2} 0008 P{0.5≤X<3}=P{X=1+P{X=2 音+品

P X  = 2 P X 0.5 3   = 例如 设离散型随机变量X 的分布律为 则 0 1 2 3 4 5 1 3 1 4 3 4 16 16 16 16 16 16 k X p 1 3 1 16 16 16 = + + 5 16 = 3 1 16 16 = + P X P X P X  = + = + = 0 1 2      P X P X  = + = 1 2    1 4 =

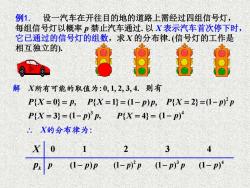
例1.设一汽车在开往目的地的道路上需经过四组信号灯， 每组信号灯以概率p禁止汽车通过.以X表示汽车首次停下时， 它已通过的信号灯的组数，求X的分布律.（信号灯的工作是 相互独立的). 8宫88 解 X所有可能的取值为：0,1,2,3,4.则有 P{X=0}=p,P{X-1}=(1-p)P,PX=2}=(1-p)'p P{X=3}=(1-p)°p, P{X=4=(1-p)4 .X的分布律为： 2 3 4 (1-p)p (1-p)2p (1-p)3p (1-p)4

例1. 设一汽车在开往目的地的道路上需经过四组信号灯， 每组信号灯以概率 p 禁止汽车通过. 以 X 表示汽车首次停下时， 它已通过的信号灯的组数，求X 的分布律. (信号灯的工作是 相互独立的). 解 则有 pk X 0 1 2 3 4 p (1 ) − p p 2 (1 ) − p p 3 (1 ) − p p 4 (1 ) − p  X的分布律为： P X{ 0} = = p， P X{ 1} = = (1 ) − p p， P X{ 2} = = P X{ 3} = = P X{ 4} = = 2 (1 ) − p p 3 (1 ) , − p p 4 (1 ) − p X所有可能的取值为：0 1 2 3 4.

二、常见离散型随机变量的概率分布 1.(0,1)分布（两点分布） 设随机变量X只可能取0与1两个值，它的分布律为 X 0 1 1-p 或：P{X=k}=p(1-p)-,k=0,10<p<1) 则称X服从(0-1)分布或两点分布. 注：任何一个只有两种可能结果的随机现象，总能定义一 个服从0,1分布的随机变量

二、常见离散型随机变量的概率分布 设随机变量X 只可能取0与1两个值, 它的分布律为 X pk 0 1− p 1 p 则称 X 服从 (0-1) 分布或两点分布. 1.（0, 1）分布（两点分布） 1 { } (1 ) , 0,1(0 1) k k P X k p p k p − 或： = = − =   注：任何一个只有两种可能结果的随机现象, 总能定义一 个服从0，1 分布的随机变量

2.伯努利试验、二项分布 Jacob Bernoulli ()伯努利试验 (16541705) 设试验E只有两个可能 Switzerland 的结果：A及A,则称E为伯努利试验 设P(A)=p(0<p<1),此时P(A)=1-p. (2)n重伯努利试验 将伯努利试验E独立地重复地进行n次，则称这一串重 复的独立试验为n重伯努利试验， 各次试验的结果互不影响 每次试验PA)=p不变

各次试验的结果互不影响 每次试验P(A)=p不变 2. 伯努利试验、二项分布 (1) 伯努利试验 设试验 只有两个可能 的结果 : 及 ,则称 为伯努利试验. E A A E (2) n 重伯努利试验 将伯努利试验 地 地进行 次 则称这一串重 复的独立试验为 独立 重复 重伯努利试验 , n . E n 设 P A p p P A p ( ) (0 1), ( ) 1 . =   = − 此时 Jacob Bernoulli （1654——1705） Switzerland

3)二项分布 若X表示n重伯努利试验中事件A发生的次数，则 X的分布律P{X=k即A在n次试验中发生k次的概率为 「Px=k3=Cp1-p)-t,k=01,2,n。} 证明：A在指定的k次(k≤)试验中发生，其它n-k次 不发生的概率为p(I-p)”- (独立性、乘法公式) 而这种指定方式共有C种， (加法公式) .P{X==C0p(I-p)- 称这样的分布为二项分布.记为X~b(n,p)

X P X 的分布律  = k即A n 在 次试验中发生k次的概率为 (3) 二项分布 若 X n A 表示 重伯努利试验中事件 发生的次数，则 A k 在 （k n n k  − ）试验中发生，其它 次 不发生 指定的 次 的概率为 (1 ) (独立性、乘法公式) k n k p p − − 证明： 称这样的分布为二项分布. 记为 , k Cn 种 (1 ) k k n k C p p n −  = = P X k { } − X b n p ~ ( , ). 而这种指定方式共有 （加法公式） P X k C p p k n { } (1 ) 0,1,2,., = = − = n k k n k−

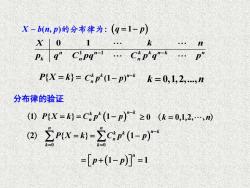
X~b(n,p)的分布律为：（q=1-p) X01 p4q”CPq-1.Chp^q"-·p P{X=k=Chp(1-p)"-k=0,1,2,.,n 分布律的验证 ()P{X=k}=C0D(（1-p)"-≥0(k=0,1,2,.,m 2Px=)-cip'(1-p) =[p+(1-p]=1

1 1 0 1 n n k k n k n k n n X k n p q C pq C p q p − − (1 ) k k n k C p p n − P X k { } = = − k n = 0,1,2,., 1 { } 1( ) n k k k P X k C p p n − （ ） = = − X b n p ~ ( , )的分布律为： ( ) 0 0 2 { } 1 n n n k k k n k k P X k C p p − = = （ ）   = = − (1 1 ) n = + − =   p p   分布律的验证  = 0 0 1 2, , （k n ， ） (q p = −1 )

例2按规定，某种型号电子元件的使用寿命超过1500小时 的为一级品.已知某一大批产品的一级品率为02，现在从 中随机地抽查20只，问20只元件中恰有k只(k=0,1,20) 一级品的概率是多少？ 分析：这是不放回抽样，由于总数很大，且抽查元件的数量 又很小，因而此抽样可近似当作放回抽样来处理， 把检查一只元件看它是否为一级品看成是一次试验， 检查20只元件相当于做20重伯努利试验. 解以X记20只元件中一级品的只数，则X~b(20,0.2), 因此所求概率为 P{X=k}=Cw(0.2)(0.8)20-,k=0,1,.,20

, 1500 . 0.2, 20 20 ( 0,1, ,20) ? k k = 按规定 某种型号电子元件的使用寿命超过 小时 的为一级品 已知 产品的一级品率为 现在从 中随机地抽查 只，问 只元件中恰有 只 一级品的概 一大批 率是多少 某 分析： , 20 20 . 把检查一只元件看它是否为一级品看成是一次试验 检查 只元件相当于做 重伯努利试验 例2 . 这是 由于总数很大，且抽查元件的数量 又很小，因而此抽样可近似当作放回抽样 不放回抽 ， 来处理 样 解 以 X 记 20 , 只元件中一级品的只数 则 X b ~ (20, 0.2), 因此所求概率为 20 20 { } (0.2) (0.8) , 0,1, ,20. k k k P X k C k − = = =